缺点数管制图
缺点数管制图概述
缺点数管制图是一种计数值管制图,能在每一批量的生产中侦测出每一零件或受验单位不良点的数目。
缺点数管制图的理论计算
所谓不合格品是指一件物品无法符合一项或多项之规格要求。任何不符合规格之处,称为一个不合格点(nonconformity)或缺点 (defect)。根据不合格点之严重性,我们可能将具有许多不合格点之物品视为合格品。换句话说,具有不合格点之物品,不一定为不合格品。 C管制图是为了管制一个检验单位之总不合格点数。在每一样本中出现不合格点之机率,服从卜瓦松分配的假设下。每个样本出现的缺点数是参数为λ的 Poisson分配,。
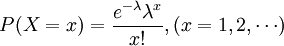
X即缺点数的随机变数,因为X设为Poisson分配,故其平均值与变异数都为λ。如果管制图上下限以3σ为准,且已知,则管制图的计算如下:
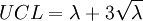
中心线 = λ
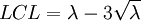
其中:UCL 表示控制图的上控制界限; LCL 表示控制图的下控制界限;
缺点数管制图的使用条件
因为c管制图在卜瓦松分配的假设下,有几项条件必须符合(Grant和Leavenworth l988,Montgomery 1991):
1.在产品出现不合格点之机会(位置)要相当大,而每一特定位置发生不合格点之机率很小且固定。
2.每一样本发生不合格点之机会(范围)要相同。
3.不合格点之发生需为独立,亦即产品上某一部分发生不合格点不影响其他不合格点之出现。
缺点数管制图的使用中可能的情形
如果λ未知,λ的不偏估计值为平均每样本上的缺点数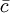 ,
,
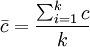
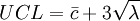
中心线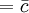
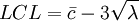
缺点数管制图实例
【例】:下表是某汽车工厂生产之车门不合格点数记录,每组样本大小为100,试建立管制图。
【解】:
此25组样本共含236个缺点,因此c之估计值为
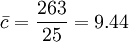
试用管制界限为
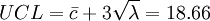
中心线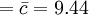
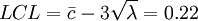
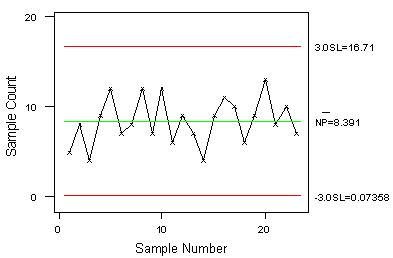
依此25组样本绘制下面管制图:
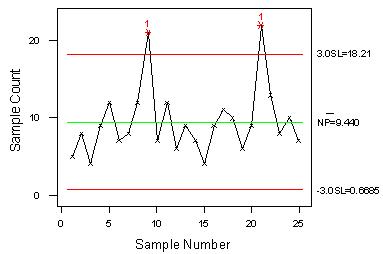
其中样本9及21均超出管制界限,因此必须诊断样本9及21之异常原因。若异常原因已排除后,则可将样本9及21之数据删除,并重新计算管制界限,新的不合格点数之平均值为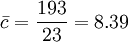 。修正后之管制界限为
。修正后之管制界限为
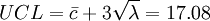
中心线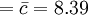
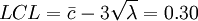
修正后管制图如下:
相关条目不良率管制图不良数管制图单位缺点管制图
缺点数管制图是一种计数值管制图,能在每一批量的生产中侦测出每一零件或受验单位不良点的数目。
缺点数管制图的理论计算
所谓不合格品是指一件物品无法符合一项或多项之规格要求。任何不符合规格之处,称为一个不合格点(nonconformity)或缺点 (defect)。根据不合格点之严重性,我们可能将具有许多不合格点之物品视为合格品。换句话说,具有不合格点之物品,不一定为不合格品。 C管制图是为了管制一个检验单位之总不合格点数。在每一样本中出现不合格点之机率,服从卜瓦松分配的假设下。每个样本出现的缺点数是参数为λ的 Poisson分配,。
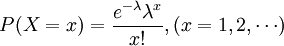
X即缺点数的随机变数,因为X设为Poisson分配,故其平均值与变异数都为λ。如果管制图上下限以3σ为准,且已知,则管制图的计算如下:
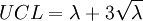
中心线 = λ
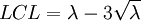
其中:UCL 表示控制图的上控制界限; LCL 表示控制图的下控制界限;
缺点数管制图的使用条件
因为c管制图在卜瓦松分配的假设下,有几项条件必须符合(Grant和Leavenworth l988,Montgomery 1991):
1.在产品出现不合格点之机会(位置)要相当大,而每一特定位置发生不合格点之机率很小且固定。
2.每一样本发生不合格点之机会(范围)要相同。
3.不合格点之发生需为独立,亦即产品上某一部分发生不合格点不影响其他不合格点之出现。
缺点数管制图的使用中可能的情形
如果λ未知,λ的不偏估计值为平均每样本上的缺点数
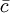 ,
,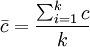
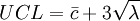
中心线
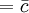
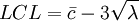
缺点数管制图实例
【例】:下表是某汽车工厂生产之车门不合格点数记录,每组样本大小为100,试建立管制图。
【解】:
此25组样本共含236个缺点,因此c之估计值为
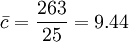
试用管制界限为
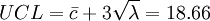
中心线
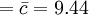
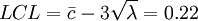
依此25组样本绘制下面管制图:

其中样本9及21均超出管制界限,因此必须诊断样本9及21之异常原因。若异常原因已排除后,则可将样本9及21之数据删除,并重新计算管制界限,新的不合格点数之平均值为
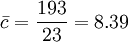 。修正后之管制界限为
。修正后之管制界限为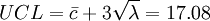
中心线
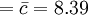
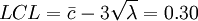
修正后管制图如下:

相关条目不良率管制图不良数管制图单位缺点管制图
附件列表
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
