加权算术平均指数
什么是加权算术平均指数
加权算术平均指数是以基期总量为权数对个体数量指标指数进行加权算术平均,以此计算的加权平均数指数等于数量指标综合指数。
加权算术平均指数的编制
加权算术平均指数=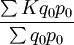
上式中,K表示数量指标的个体指数,表示基期的某个总量指标。也就是说,要编制加权算术平均数指数,一要掌握数量指标个体指数,二要掌握基期总量。
当已知数量指标的个体指数Kq,或报告期与基期的个体数量指标ql、q0,以及基期的总量指标(产值或销售额)p0q0并以其作为权数时;同样,已知质量指标的个体指数kp,或报告期与基期的个体价格指标p1、p0 及报告期的总量指标(产值或销售额)p1q1为权数时,即可分别计算数量指标的总指数及质量指标的总指数 。即:
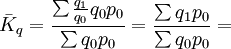 数量指标综合指数
数量指标综合指数
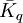 :为加权平均数量指标指数;
:为加权平均数量指标指数;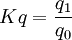 为数据指标的个体指数。
为数据指标的个体指数。
由上式可知,在一定条件下,加权算术平均指数是拉氏综合指数的变形。同时只有用q0p0为权数的情况下加权,加权算术平均指数才可能与拉氏综合指数相互转换变为综合指数。如果权数不是P0q0,而使用p0q0以外的任何其它权数进行加权,加权算术平均指数就不可能等于综合指数,当然,这种变形关系也就不复存在。
在用拉氏综合指数公式计算商品销售量指数时,必须掌握基期和报告期各种商品的销售量及基期各种商品的价格资料。但在实践中,按基期价格与报告期销售量所计算的假定销售额(p0ql)资料不易取得,而基期的销售额资料(p0q0)与各种商品的销售量个体指数却很容易取得。所以,加权算术平均指数适用于数量指标平均数指数的计算。
加权算术平均指数是以基期总量为权数对个体数量指标指数进行加权算术平均,以此计算的加权平均数指数等于数量指标综合指数。
加权算术平均指数的编制
加权算术平均指数=
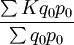
上式中,K表示数量指标的个体指数,表示基期的某个总量指标。也就是说,要编制加权算术平均数指数,一要掌握数量指标个体指数,二要掌握基期总量。
当已知数量指标的个体指数Kq,或报告期与基期的个体数量指标ql、q0,以及基期的总量指标(产值或销售额)p0q0并以其作为权数时;同样,已知质量指标的个体指数kp,或报告期与基期的个体价格指标p1、p0 及报告期的总量指标(产值或销售额)p1q1为权数时,即可分别计算数量指标的总指数及质量指标的总指数 。即:
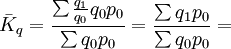 数量指标综合指数
数量指标综合指数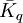 :为加权平均数量指标指数;
:为加权平均数量指标指数;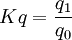 为数据指标的个体指数。
为数据指标的个体指数。由上式可知,在一定条件下,加权算术平均指数是拉氏综合指数的变形。同时只有用q0p0为权数的情况下加权,加权算术平均指数才可能与拉氏综合指数相互转换变为综合指数。如果权数不是P0q0,而使用p0q0以外的任何其它权数进行加权,加权算术平均指数就不可能等于综合指数,当然,这种变形关系也就不复存在。
在用拉氏综合指数公式计算商品销售量指数时,必须掌握基期和报告期各种商品的销售量及基期各种商品的价格资料。但在实践中,按基期价格与报告期销售量所计算的假定销售额(p0ql)资料不易取得,而基期的销售额资料(p0q0)与各种商品的销售量个体指数却很容易取得。所以,加权算术平均指数适用于数量指标平均数指数的计算。
附件列表
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
