模糊决策法
模糊決策法(Fuzzy Decision Method)
什么是模糊决策法
模糊决策是决策的要素(如准则及备选方案等) 具有模糊性的决策。而模糊决策法是指运用模糊数学方法来处理一些复杂的决策问题。这类问题一般具有大系统特征,系统之间的关系十分复杂,存在不能准确赋值的变量,这些变量属于模糊因素,涉及到一定的主观因素,使得子系统之间、变量之间的关系不清晰,从而必须借助排序、模糊评判等方法来进行处理。
在现实生活中,很多概念都是模糊的。如高个子,身高达到多少即算高个子,并无明确的定义,不同的人会有不同的理解。另外如应聘的能力、工作态度、性格等概念也是模糊的。这些概念的内涵是明确的,但外延是模糊的。在企业招聘的现实中,很多指标概念是模糊的,因此模糊决策法正在成为企业招聘决策中的一种很有实用价值的工具。
模糊决策法的案例分析
案例:模糊决策法在物流顾客服务中的应用
结合下表来自化工行业某一细分市场的数据来说明进行竞争性对比分析的定量方法。这里分析两家企业A和B的情况,其产品为日用消费品,顾客特指零售商及其他中间商。设x为企业的业绩得分,Y为医素的重要性得分,2为相对业绩得分(A相对于B)。论壤x为表1中的要素。
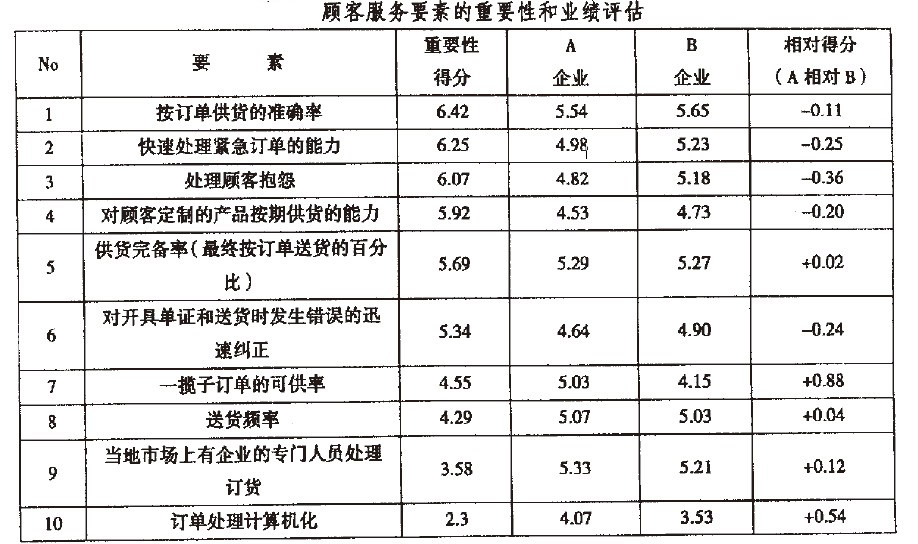
1.业绩评价分析
(1)建立函数
令模糊集A1表示“必须改进”,A2表示“改进服务”,A3表示“保持服务”,A4表示“降低,保持服务”,A5表示“降低服务”。它们是论域X上的模糊集,其隶属函数规定如下:
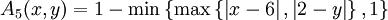 |6-y\right|\right\},1\right\} src="uploads/201202/1330059031GvA9aC5Y.png">|
|6-y\right|\right\},1\right\} src="uploads/201202/1330059031GvA9aC5Y.png">|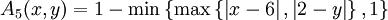 |6-y\right|\right\},1\right\} src="http://wiki.mbalib.com/w/images/math/f/e/f/fefe684da0602dae84fb500f9c74a85c.png">
|6-y\right|\right\},1\right\} src="http://wiki.mbalib.com/w/images/math/f/e/f/fefe684da0602dae84fb500f9c74a85c.png">
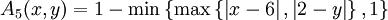 |6-y\right|\right\},1\right\})\lor(1-\min\left\{\max\left\{\left|
|6-y\right|\right\},1\right\})\lor(1-\min\left\{\max\left\{\left|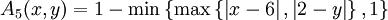 |6-y\right|\right\},1\right\} src="uploads/201202/1330059031GvA9aC5Y.png">|
|6-y\right|\right\},1\right\} src="uploads/201202/1330059031GvA9aC5Y.png">|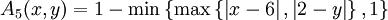 |4-y\right|\right\},1\right\}) src="http://wiki.mbalib.com/w/images/math/b/b/d/bbd7bb08a7f8a5787369442019e5fdc2.png">
|4-y\right|\right\},1\right\}) src="http://wiki.mbalib.com/w/images/math/b/b/d/bbd7bb08a7f8a5787369442019e5fdc2.png">
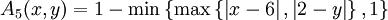 |6-y\right|\right\},1\right\} src="uploads/201202/1330059031GvA9aC5Y.png">|
|6-y\right|\right\},1\right\} src="uploads/201202/1330059031GvA9aC5Y.png">|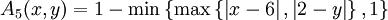 |2-y\right|\right\},1\right\})\lor(1-\min\left\{\max\left\{\left|x-4\right|
|2-y\right|\right\},1\right\})\lor(1-\min\left\{\max\left\{\left|x-4\right|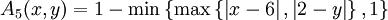 |4-y\right|\right\},1\right\})\lor(1-\min\left\{\max\left\{\left|x-6\right|
|4-y\right|\right\},1\right\})\lor(1-\min\left\{\max\left\{\left|x-6\right|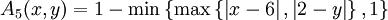 |6-y\right|\right\},1\right\}) src="http://wiki.mbalib.com/w/images/math/9/5/3/953d28c61bf0669f95cef43cd7ab9fc2.png">
|6-y\right|\right\},1\right\}) src="http://wiki.mbalib.com/w/images/math/9/5/3/953d28c61bf0669f95cef43cd7ab9fc2.png">
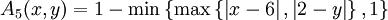 |4-y\right|\right\},1\right\})\lor(1-\min\left\{\max\left\{\left|x-4\right|
|4-y\right|\right\},1\right\})\lor(1-\min\left\{\max\left\{\left|x-4\right|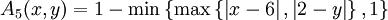 |2-y\right|\right\},1\right\}) src="uploads/201202/1330059031I736QI47.png">
|2-y\right|\right\},1\right\}) src="uploads/201202/1330059031I736QI47.png">
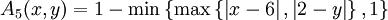 |2-y\right|\right\},1\right\} src="http://wiki.mbalib.com/w/images/math/6/d/a/6dacc40263bbd9420a6660cbcb05c9fc.png">
|2-y\right|\right\},1\right\} src="http://wiki.mbalib.com/w/images/math/6/d/a/6dacc40263bbd9420a6660cbcb05c9fc.png">
(2)模式识别
对十个要素进行模式识别,分别求解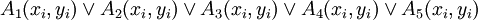 ,其中xi和yi分别表示第i个要素的业绩得分和重要性得分。
,其中xi和yi分别表示第i个要素的业绩得分和重要性得分。
对于A企业的第一个因素x1 = 6.42,y1 = 5.54。解得
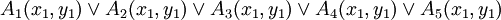
所以,要素l按订单订货的准确率应保持现有服务水平。
同理,由模糊识别法得要素2、3、4、6需改进服务,要素7、8、9、10需降低,保持服务,要素5保持服务。且
A2(x2,y2) = 0.02,A2(x3,y3) = 0.18 A2(x4,y4) = 0.47,A3(x5,y5) = 0.29,
A2(x6,y6) = 0.34,A4(x7,y7) = 0.03 A4(x8,y8) = 0.07,A4(x9,y9) = 0.33,
A4(x10,y10) = 0.70
2.竞争地位分析
(1)建立函数
令模糊集B1表示“重要”,B2表示“比较重要”,B3表示“不重要”。C1表示“竞争优势”,C2表示“优势对等”,C3表示“竞争劣势”。其隶属函数规定如下:
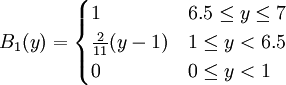
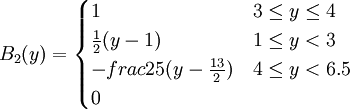
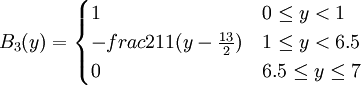
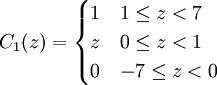
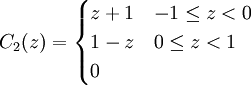
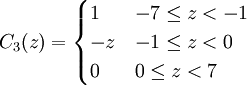
(2)模式识别
对十个要素进行模式识别,分别求解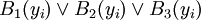 以及
以及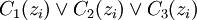 ,其中yi和zi,分别表示第i个要素的重要性得分和相对业绩得分。
,其中yi和zi,分别表示第i个要素的重要性得分和相对业绩得分。
对于A企业的第一个因素y1 = 5.54,z1 = − 0.11,解得
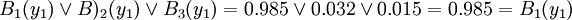
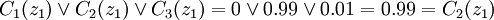
所以,要素1很重要,而在此要素上4企业与B企业相比处于优势对等。
同理可得要素2,3,…,6很重要,而且在这些要索上A企业与口企业业绩相比处于优势对等。A企业应当改进编号为1,2,…,6的服务要素的服务水平,持续改进所需的费用肯定低于因此而增加的收益。要素7比较重要,而在要素7上A企业与B企业相比处于竞争优势。A企业应当适当降低要素7的服务水平,与其重要性相当,从而可降低成本。要素8,9比较重要,同时在这两个要素上A企业与B企业相比处于优势对等。A企业应继续保持其服务水平。要索IO不重要,但A企业与B企业相比处于竞争优势。
故A企业应适当降低要素10的服务投人。由以上分析可知A企业需提高要素1,2,…,6服务水平,使其更具竞争力;同时降低要素7、10的服务水平,减少成本;而要素8、9继续保持原来的服务水平。
3.总结
由2的结论知,A企业管理层应当增加对要素l,2,…,6的投入以使之变为主要值争)能力。这六个要素都提供了相当大的机会;然而,由1的结果可知,要素2、3、4、6的改进更能增强企业的竞争优势。要素l最受顾客重视,但A企业及其主要竞争对手B企业的服务业绩得分都不十分出色,这就是一个改进服务的机会。因为A企业在要素5上的服务业绩与顾客的期望值十分接近,要素5改进的潜力远不如要素l、2、3、4和6,所以保持要素5的服务水平不变。
由以上分析可知,提高要素l、2、3、4和6的服务水平,使之更具竞争能力,其中要素2和4还可能变成主要竞争能力并成为竞争优势的主要源泉。如果将要索1、3、5、6发展为主要竞争能力,则必须加强顾客对这些要素的重要性评价,否则会导致A企业在这些方面的服务水平超越顾客的期望而显得过高。由1知要素7、8、9、10的服务水平都可以适当降低,但由2知,降低一企业对要素8、9、10的服务水平可能导致相对于占企业的竞争劣势。故对这四个要素的分析应结合它们的具体内容。
对于要素7,A企业应当降低服务水平,但如果有一部分特殊的顾客十分重视该要素的话,则应当针对这一特殊的顾客群体加强要素7的服务;对于要素8,一企业应当告知顾客并使之相信小批量高频率的送货是十分重要的,优于大批量低频率的送货;事实上顾客之所以忽视该要素是因为他们认为大批量低频率供货稳定性好,有利于计划工作;对于要素9,企业应让顾客相信该要素是不必要的,从而企业可减少这方面的开支;对于要素10.应根据顾客群体的分类来决策,对购买量大、企业获利高的大客户,应加强该要素,对普通的小客户则可以减少这方面的开支。
