调和平均数
调和平均数概述
调和平均数又称倒数平均数,是变量倒数的算术平均数的倒数。
调和平均数的计算公式
调和平均数是给定数据的倒数之算术平均数的倒数。
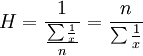 (简单平均式)
(简单平均式)
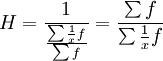 (加权平均式)
(加权平均式)
调和平均数的特点
1、调和平均数易受极端值的影响,且受极小值的影响比受极大值的影响更大。
2、只要有一个变量值为零,就不能计算调和平均数。
3、当组距数列有开口组时,其组中值即使按相邻组距计算了,假定性也很大,这时,调和平均数的代表性就很不可靠。
4、调和平均数应用的范围较小。
调和平均数与算术平均数的比较
(一)调和平均数与算术平均数的区别
变量不同:算术平均数是x,调和平均数是 1/x 。
权数不同:算术平均数是f或n,代表次数(单位数),调和平均数是xf或M,代表标志总量。
(二)调和平均数与算术平均数的联系:调和平均数作为算术平均数的变形使用:
∵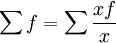
∴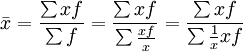
令 M=xf
则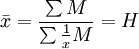
应用调和平均数应注意问题
1、变量x的值不能为0。
2、调和平均数易受极端值的影响。
3、要注意其运用的条件。调和平均数多用于已知分子资料,缺分母资料时。
调和平均数与算术平均数的举例分析
例一 水果甲级每元1公斤,乙级每元1.5公斤,丙级每元2公斤。问:
(1)若各买1公斤,平均每元可买多少公斤?
(2)各买6.5公斤,平均每元可买多少公斤?
(3)甲级3公斤,乙级2公斤,丙级1公斤,平均每元可买几公斤?
(4)甲乙丙三级各买1元,每元可买几公斤?
解:例一
(1)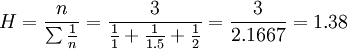 (公斤/元)
(公斤/元)
(2)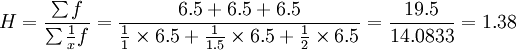 (公斤/元)
(公斤/元)
(3)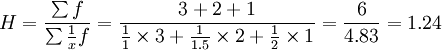 (公斤/元)
(公斤/元)
(4)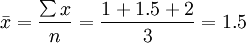 (公斤/元)
(公斤/元)
调和平均数又称倒数平均数,是变量倒数的算术平均数的倒数。
调和平均数的计算公式
调和平均数是给定数据的倒数之算术平均数的倒数。
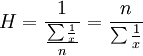 (简单平均式)
(简单平均式)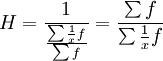 (加权平均式)
(加权平均式)调和平均数的特点
1、调和平均数易受极端值的影响,且受极小值的影响比受极大值的影响更大。
2、只要有一个变量值为零,就不能计算调和平均数。
3、当组距数列有开口组时,其组中值即使按相邻组距计算了,假定性也很大,这时,调和平均数的代表性就很不可靠。
4、调和平均数应用的范围较小。
调和平均数与算术平均数的比较
(一)调和平均数与算术平均数的区别
变量不同:算术平均数是x,调和平均数是 1/x 。
权数不同:算术平均数是f或n,代表次数(单位数),调和平均数是xf或M,代表标志总量。
(二)调和平均数与算术平均数的联系:调和平均数作为算术平均数的变形使用:
∵
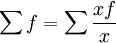
∴
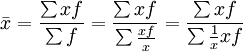
令 M=xf
则
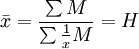
应用调和平均数应注意问题
1、变量x的值不能为0。
2、调和平均数易受极端值的影响。
3、要注意其运用的条件。调和平均数多用于已知分子资料,缺分母资料时。
调和平均数与算术平均数的举例分析
例一 水果甲级每元1公斤,乙级每元1.5公斤,丙级每元2公斤。问:
(1)若各买1公斤,平均每元可买多少公斤?
(2)各买6.5公斤,平均每元可买多少公斤?
(3)甲级3公斤,乙级2公斤,丙级1公斤,平均每元可买几公斤?
(4)甲乙丙三级各买1元,每元可买几公斤?
解:例一
(1)
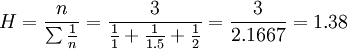 (公斤/元)
(公斤/元)(2)
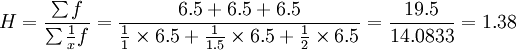 (公斤/元)
(公斤/元)(3)
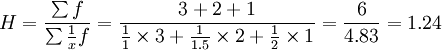 (公斤/元)
(公斤/元)(4)
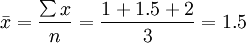 (公斤/元)
(公斤/元)附件列表
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
