投入产出表
什么是投入产出表
投入产出表(部门联系平衡表)，是指以产品部门分类为基础的棋盘式平衡表，用于反映国民经济各部门的投入和产出、投入的来源和产出的去向，以及部门与部门之间相互提供、相互消耗产品的错综复杂的技术经济关系。
投入产出表的产生
投入产出表在二十世纪三十年代产生于美国，它是由美国经济学家、哈佛大学教授瓦西里·列昂惕夫（W.Leontief）在前人关于经济活动相互依存性的研究基础上首先提出并研究和编制的。
列昂惕夫从1931年开始研究投入产出技术，编制投入产出表，目的是研究美国的经济结构。1936年他撰写的“美国经济制度中投入产出数量关系”在《经济学和统计学评论》上发表。它是世界上有关投入产出技术的第一篇论文，标志着投入产出技术的诞生。1953年列昂惕夫与他人合作，出版了《美国经济结构研究》一书。通过这些论著，列昂惕夫提出了投入产出表的概念及其编制方法，阐述了投入产出技术的基本原理，创立了投入产出技术这一科学理论。正是在投入产出技术方面的卓越贡献，列昂惕夫于1973年获得了第五届诺贝尔经济学奖。
投入产出表的发展
投入产出技术从诞生到现在的七十多年里，无论是在理论方面，还是在实践方面都得到了很大的发展，取得了丰硕成果。早期的投入产出模型，只是静态的投入产出模型。后来，随着研究的深入，开发了动态投入产出模型，投入产出技术由静态扩展到动态。近期，随着投入产出技术与数量经济方法等经济分析方法日益融合，投入产出分析应用领域不断扩大。
五十年代末六十年代初，我国经济理论界和一些高等院校的少数同志开始研究投入产出技术，某些高等院校还开设了投入产出技术课程。“文革”期间，此项工作几乎中断。1974年8月，为研究宏观经济发展情况的需要，在国家统计局和国家计委的组织下，由国家统计局、国家计委、中国科学院、中国人民大学、原北京经济学院等单位联合编制了1973年全国61种产品的实物型投入产出表。利用该表开展的应用工作，在制定投资计划和产品生产计划等方面发挥了积极的作用。
十一届三中全会以后，党和国家把工作重点放到经济建设上，这就为包括投入产出技术在内的现代经济分析方法的研究和应用创造条件。从此开始投入产出表的编制工作，投入产出技术的研究和投入产出表的应用工作得到了迅速的发展。
1980年，按照国家统计局的要求，山西省统计局编制了山西省1979年投入产出表，为编制全国投入产出表提供了经验。
1982年，国家统计局、国家计委及有关部门编制了1981年全国投入产出价值表和实物表。
1984年，在1981年全国投入产出价值表的基础上，国家统计局编制了1983年全国投入产出延长表。
1987年，除个别地区外，各省(自治区、直辖市)都编制了本地区投入产出表；一些管理部门还编制厂部门投入产出表；一些企业也编制了企业投入产出表。
1987年3月底，为了适应改革开放的需要，为加强国民经济宏观调控和管理，提高经济决策的科学性，国务院办公厅发出了《关于进行全国投入产出调查的通知》（国办发18号），明确规定每五年（逢二、逢七年份）进行一次全国投入产出调查和编表工作。1987年，我国进行了第一次全国性的投入产出调查和编表工作。《1987年全国投入产出表》的编制成功和在宏观经济调控等方面的成功应用，标志着投入产出技术在我国发展到一个新的阶段。
1992年，国家统计局在1987年全国投入产出表的基础上，编制了1990年投入产出延长表。
1994年和1995年，国家统计局先后编制了1992年全国出价值表和实物表。1992年全国投入产出表为国民经济核算体系全面转轨提供了数据依据。
1996年，国家统计局在1992年全国投入产出表的基础上，编制了1995年全国投入产出延长表。
1999年，国家统计局编制了1997年全国投入产出表。
到目前为止，除西藏以外，全国三十个省(自治区、直辖市)与国家同步编制了1987、1992和1997年本地区投入产出表。部分省(自治区、直辖市)还编制了1990年、1995年和2000年本地区投入产出延长表。今年开始进行第五次全国投入产出调查，并编制2007年全国投入产出表。
投入产出技术不仅在我国宏观和微观经济领域获得了广泛的应用，而且在微观经济领域的应用也取得了可喜的成绩。目前，已有一些企业编制了企业投入产出表，并用于企业计划、生产、成本等管理工作中。
">编辑] 投入产出表的分类按计量单位分：价值型和实物型；按表式结构分：对称型(纯部门)和U-V型(UV表法)；按资料范围分：全国表、地区表和企业表；按时间期限分，静态表和动态表；按考察领域分：产品表，固定资产表、能源表、人口表、教育表、环境污染表，等等。投入产出表基本结构
投入产出表由供给表、使用表和产品部门×产品部门表组成。供给表又称产出表，主栏为n个产品部门，宾栏为m个产业部门，沿行方向看，反映属于某一产品部门的货物或服务是由哪些产业部门生产的，合计为属于该产品部门的货物或服务的总产出；沿列方向看，反映某一产业部门生产各产品部门货物或服务的价值量，合计为该产业部门总产出。全部产业部门总产出等于全部产品部门总产出。通常产品部门个数多于产业部门个数。按生产者价格计算的总供给等于按生产者价格计算的总产出与进口之和；按购买者价格计算的总供给等于按生产者价格计算的总供给与商业和运输费用之和。
使用表又称投入表，通常由三部分组成，第一部分的主栏包括n个产品部门，宾栏包括m个产业部门。沿行方向看，表明各产品部门生产的货物或服务提供给各产业部门使用的价值量，沿列方向看，表明各产业部门从事生产活动所消耗各产品部门生产的货物或服务的价值量；第二部分是第一部分在水平方向上的延伸，其主栏与第一部分相同，也是n个产品部门，其宾栏由最终消费、资本形成总额、出口等最终使用项组成，它反映各产品部门生产的货物或服务用于最终使用的价值量及其构成；第三部分是第一部分在垂直方向上的延伸，其主栏由劳动者报酬、生产税净额、固定资产折旧和营业盈余等增加值项组成，宾栏与第一部分的宾栏一致，也是m个产业部门，它反映各产业部门增加值的构成情况。
产品部门×产品部门表，形式上与使用表相似，也是由三部分组成，第一部分是由名称相同、排列次序相同、数目一致的n个产品部门纵横交叉而成的，其主栏为中间投入、宾栏为中间使用，它充分揭示了国民经济各产品部门之间相互依存、相互制约的技术经济联系，反映了国民经济各部门之间相互依赖、相互提供劳动对象供生产和消耗的过程。沿行方向看，反映第i产品部门生产的货物或服务提供给第j产品部门使用的价值量；沿列方向看，反映第j产品部门在生产过程中消耗第i产品部门生产的货物或服务的价值量。第二部分是第一部分在水平方向上的延伸，其主栏与第一部分的主栏相同，也是n个产品部门；其宾栏由最终消费、资本形成总额、出口等最终使用项组成。它反映各产品部门生产的货物或服务用于各种最终使用的价值量及其构成。第三部分是第一部分在垂直方向上的延伸，其主栏由劳动者报酬、生产税净额、固定资产折旧和营业盈余等增加值项组成；宾栏与第一部分的宾栏相同，也是n个产品部门，它反映各产品部门增加值的构成情况。
产品部门×产品部门表的平衡关系是：
从纵列方向看，第j产品部门中间投入合计＋第j产品部门增加值合计＝第j产品部门总投入
从横行方向看，第i产品部门中间使用合计＋第i产品部门最终使用合计－第i产品部门进口＝第i产品部门总产出
从总量看，总投入＝总产出
第i产品部门总投入＝第i产品部门总产出
中间投入合计＝中间使用合计
投入产出表编制方法
投入产出表的编制方法主要指编制产品部门×产品部门表的方法。产品部门×产品部门表有两种编制方法，一种是间接推导法，另一种是直接分解法。
间接推导法是以产业活动单位为统计单位，按照产业活动单位主产品的性质将其划分到某一产业部门，并编制包括全部产业部门在内的使用表和供给表，然后利用使用表和供给表，依据一定的假定，采用数学方法推导出产品部门×产品部门表的方法。
间接推导法使用的假定有两种，一是产品工艺假定，即假定不管由哪个产业部门生产，同一种产品具有相同的投入结构；二是产业部门工艺假定，即假定同一产业部门不论生产何种产品，都具有相同的投入结构。
直接分解法与间接推导法不同，其统计单位不是产业活动单位，而是一个企业。一个企业，特别是大中型企业，往往同时生产几种、甚至几十种不同质的产品，它们的投入构成不同，根据产品部门的要求，将该企业生产的各种产品，按其性质划归到相应产品部门中，利用企业按产品部门直接分解后的投入构成资料，编制产品部门×产品部门表的方法。
目前我国采用的是以直接分解法为主，间接推导法为辅的编表方法。
">编辑] 投入产出表的四大象限
暂不考虑作为合计数的“总投入”行与“总产出”列以及生产部门的“小计”栏，可将投入产出表划分为四大象限，分别表达特定的经济内容。
（1）第Ⅰ象限(中间产品或中间消耗)：核心。反映各部门之间相互提供、相互消耗产品的技术经济联系。
第Ⅰ象限的特点：
横行标题和纵栏标题是名称、排序相同的产品部门，具有严整的棋盘式结构；横行～提供中间产品的部门(产出部门)；纵栏～消耗中间产品的部门(投入部门)；表中每项数据都具有“产出”与“消耗”的双重涵义。该象限的所有n2 个数据组成“中间流量(中间产品、中间消耗)矩阵”：
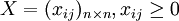
(2)第Ⅱ象限(最终产品或最终使用)：反映各部门提供最终产品的数量和构成情况（可以细分为消费、投资和净出口）。
其数据组成“最终产品列向量”：
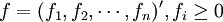
(3)第Ⅲ象限(最初投入或增加值)：反映各部门的最初投入数量及其构成（可以细分）。其数据组成“最初投入(增加值)行向量”：
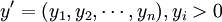
(4)第Ⅳ象限：空白（可在国民核算矩阵中适当开发）。
">编辑] 投入产出表的两个方向
横表：Ⅰ＋Ⅱ，反映各部门的产出及其使用去向，即“产品分配”过程；
竖表：Ⅰ＋Ⅲ，反映各部门的投入及其提供来源，即“价值形成”过程。
“横表”和“竖表”各自存在一定的平衡关系，彼此之间又在总量上相互制约，构成投入产出表建模分析的基础框架。
">编辑] 投入产出表的平衡关系
投入产出表的基本平衡关系有如下三种:
（一）各行(横表)的平衡──产品平衡方程：
中间产品＋最终产品＝总产出
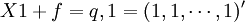
（二）各列(竖表)的平衡──价值平衡方程：
中间投入＋最初投入＝总投入
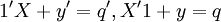
（三）各行列(横表和竖表)的对应平衡：
各部门总产出＝该部门总投入
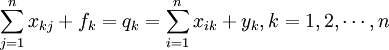
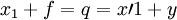
这表明：“产品平衡方程”与“价值平衡方程”既相对独立，又相互制约。
从投入产出表所有行列的角度看，有：
所有部门的总产出＝所有部门的总投入，即:
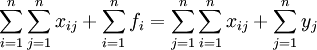
所有部门的中间产品＝所有部门的中间消耗，即:
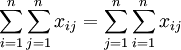
从而有:
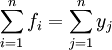
即：所有部门提供的最终产品＝所有部门创造的增加值。
但应注意：
每个部门所提供的中间产品价值与其消耗的中间产品价值通常不等，即：
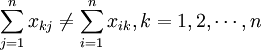
每个部门所提供的最终产品价值与其创造的增加值通常也不等，即：
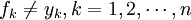
投入产出表的作用
投入产出表可全面系统地反映国民经济各部门之间的投入产出关系，揭示生产过程中各部门之间相互依存和相互制约的经济技术联系。一方面它能告诉人们国民经济各部门的产出情况，以及这些部门的产出是怎样分配给其它部门用于生产或怎样分配给居民和社会用于最终消费或出口到国外的；另一方面它还能告诉人们，各部门为了自身的生产又是怎样从其它部门取得中间投入产品及其最初投入的状况。投入产出核算的功能不仅仅在于反映现各个部门在生产过程中直接的、较为明显的经济技术联系，更重要的是它揭示出各部门之间间接的、较为隐蔽的、甚至被人忽视的经济技术联系。投入产出表为研究产业结构，尤其为制定和检查国民经济计划，研究价格决策，进行各种定量分析提供依据。
投入产出表的主要系数
投入产出系数是进行投入产出分析的重要工具。投入产出系数包括直接消耗系数、完全消耗系数、感应度系数、影响力系数和各种诱发系数。由于直接消耗系数和完全消耗系数是最基本的投入产出系数，这里只介绍直接消耗系数和完全消耗系数的定义和计算方法。
1、直接消耗系数
直接消耗系数，也称为投入系数，记为aij(i,j=1,2,…,n),它是指在生产经营过程中第j产品(或产业)部门的单位总产出所直接消耗的第i产品部门货物或服务的价值量，将各产品(或产业)部门的直接消耗系数用表的形式表现就是直接消耗系数表或直接消耗系数矩阵，通常用字母A表示。
直接消耗系数的计算方法为：用第j产品(或产业)部门的总投入Xj去除该产品部门(或产业)生产经营中所直接消耗的第i产品部门的货物或服务的价值量Xij,用公式表示为:
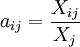(i,j=1,2,…,n)
直接消耗系数体现了列昂惕夫模型中生产结构的基本特征，是计算完全消耗系数的基础。它充分揭示了国民经济各部门之间的技术经济联系，即部门之间相互依存和相互制约关系的强弱，并为构造投入产出模型提供了重要的经济参数。
从直接消耗系数的定义和计算方法可以看出，直接消耗系数的取值范围在0≤aij＜1之间，aij越大，说明第j部门对第i部门的直接依赖性越强；aij越小，说明第j部门对第i部门的直接依赖性越弱；aij = 0则说明第j部门对第i部门没有直接的依赖关系。
2、完全消耗系数
完全消耗系数是指第j产品部门每提供一个单位最终使用时，对第i产品部门货物或服务的直接消耗和间接消耗之和。将各产品部门的完全消耗系数用表的形式表现出来，就是完全消耗系数表或完全消耗系数矩阵，通常用字母Ｂ表示。完全消耗系数的计算公式为：
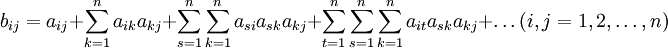
式中的第一项aij表示第j产品部门对第i产品部门的直接消耗量；式中的第二项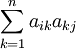
表示第j产品部门对第i产品部门的第一轮间接消耗量；式中的第三项
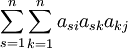为第二轮间接消耗量；式中的第四项
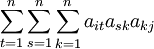为第三轮间接消耗量；依此类推，第n+1项为第n轮间接消耗量。按照公式所示，将直接消耗量和各轮间接消耗量相加就是完全消耗系数。
完全消耗系数矩阵可以在直接消耗系数矩阵的基础上计算得到的，利用直接消耗系数矩阵计算完全消耗系数矩阵的公式为：
B = (I − A) − 1 − I
式中的A为直接消耗系数矩阵，I为单位矩阵，为完全消耗系数矩阵。
完全消耗系数，不仅反映了国民经济各部门之间直接的技术经济联系，还反映了国民经济各部门之间间接的技术经济联系，并通过线性关系，将国民经济各部门的总产出与最终使用联系在一起。
基于投入产出表的案例分析 ">编辑] 案例一:基于投入产出表的实证分析
一、计算的理论基础
计算和分析基于投入产出表。投入产出表由三部分组成，按照左上、右上、左下的顺序，分别称为第一、第二和第三象限。其中第一象限反映了一定时期内各产业相互间的供给与需求关系，是投入产出表中最主要的部分。
第一象限的列向量（例如第j列）为产业j的投入结构，即产业j在经济活动中所消耗的其他产业的中间产品值，这反映了产业j的价值形成过程，可揭示产业j对其他产业的拉动程度。利用列向量的值可以计算中间投入率(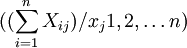
,其含义为产业j总产出中消耗其他产业中间产品的比重。
中间投入率越高的产业，增加值越低。第一象限的行向量（例如第i行）为产业f的使用结构，即在经济活动中产业i为其他产业提供的中间产品值，可揭示哪些产业是产业i的主要服务对象。利用行向量的值可计算中间需求率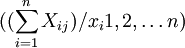
,其含义其他产业消耗产业0的中间产品占产业0的总产出的比重。中间需求率越高，对其他产业的推动力或制约性越强。
利用公式αij = Xij / xj可将第一象限的数值转化为直接消耗系数矩阵(A),元素αij称为直接消耗系数，其经济含义与上面的分析一致。直接消耗系数矩阵是本文分析的重要基础。
投入产出表是一张平衡表，表中行平衡关系式为：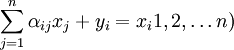
(1)
其中\alpha_{ij}就为直接消耗系数。
公式(1)表示为矩阵形式为：
AX + Y = X = > X = (I − A) − 1Y (2)
公式(2)中的(I − A) − 1称为里昂剔夫逆矩阵，利用它可以计算产业j感应度系数和影响力系数：。
感应度系数: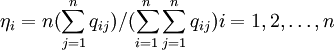
。
影响力系数: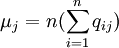
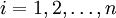
公式中qij是里昂剔夫逆矩阵(I − A) − 1中的第i行第j列的元素。影响力系数反映当产业i每增加一个单位最终使用对其他产业所产生的需求波及程度，其值大于1时，表示产业i的这种需求波及程度高于社会平均水平。感应系数反映每个产业均增加一个单位最终使用时，产业i由此而受到的需求感应程度，其值大于1时，表示产业i所受到的感应程度高于社会平均水平。
二、计算结果及分析
（一）金融保险业在上海各产业中所处的地位分析
金融保险业实现的增加值高，对其他产业的拉动性相对较弱。下表中，上海金融保险业在2002年的中间投入率为39.99%，即金融保险业每实现一单位产出，需要消耗关联产业0.3999单位的中间产品（位列同期42部门的36位，位次较低），同时实现0.6001单位的增加值，实现的增加值是中间投入的1.50倍。
进一步看，金融保险业2002年影响力系数为0.72，即金融保险业每增加%万元最终单位使用时，对其他产业所产生的生产需求为7200元，低于社会平均水平，位列同期42个部门中36名。由此可知金融保险业的增加值高，对其他产业的拉动性相对较弱。需指出，上述两个指标与1997年相比都有所下降。
金融保险业在上海各产业中所处的地位
金融保险业对其他产业的推动性较大，2002年，上海金融保险业的中间投入率为71.40%，即金融保险业总产出的71.40%要作为中间产品提供给关联产业使用，这在同期42个部门中位列21位。进一步，金融保险业2002年感应度系数为%1!3，即其他产业均增加%万元最终使用时，需金融保险业提供的服务产值为1.26万元，高于社会平均水平。从位次来看，这一数值在42个部门中位列5名。这表明金融保险业对其他产业的推动性较大，在经济产业链中处于核心地位。与1997年相比，除中间需求率有所提高外（97年为64.68%），其他都有所下降，这同样表明上海金融保险业近几年发展相对较慢。
总体上看，上海金融保险业对其他产业的拉动性弱，推动力强。拉动性弱主要因为金融保险业是一个高增加值产业；推动力强则表明了金融保险业有着相对重要的产业地位。
（二）上海金融保险业对其他产业的依赖性分析
本部分对直接消耗系数矩阵中金融保险业列向量进行排序，并进一步计算金融保险业在这些产业的中间需求中所占比重和位次，因篇幅所限，这里只在表2中展示位于前10名的产业。上述计算可以反映金融保险业对其他产业的依赖程度。这里总结出三点结论：
金融保险业的发展离不开第三产业的支持。
由表2可知，在金融保险业2002年最为依赖的前10个产业中，第三产业占了8个（前5个产业都为第三产业），比1997年多出3个。经计算，在年金融保险业的中间投入中，第三产业所占比重高达81.64%，高出第二产业4.45倍，由此可见金融保险业的发展离不开第三产业的支持。事实上，金融保险业相比2002年更加需要第三产业的支持，因为不但在年金融保险业最为依赖的个产业中第三产业的个数比年多出3个，更为重要的是，整个金融保险业中间投入中第三产业的占比（81.64%）也要比1997年（62.58%）有大幅度提高。进一步分析，对于年金融保险业最为依赖的个第三产业，金融保险业也是它们的主要服务对象，因为年金融保险业在这个第三产业的中间使用中的比重都较大，从位次上看，除交通运输及仓储业和租赁业和商务服务业外，其他产业的比重、位次都居前名。同样相比年比重和位次都有一定程度的提高，这也与前面的分析相一致（见下表）
金融保险业主要依赖的产业
金融保险业的协作依存程度高。2002年，金融保险业对本部门的直接消耗系数占金融保险业中间投入的比重为35.26%，位居42部门首位，远远高于第二名信息传输、计算机服务和软件业的10.98%，由此可见金融保险业对本部门的依赖性强，协作依存程度高。事实上，从上表中可以看出，这一情况在年就已很明显（比重为，为列首位）。从金融保险业提供中间产品的角度也可得以证明，金融保险业2002年有10.67%的中间产品提供给本部门使用，这一比重仅小于房地产业的11.33%（见上表）。金融保险业的发展是建立在完善金融体系，即众多的金融机构和高效的金融市场之上的。优惠的政策，良好的投资环境和快速健康发展的经济吸引了国内外的众多金融机构，在上海形成了银行、保险公司、证券公司、基金管理公司等多种金融机构以及银行间同业拆借和债券市场、外汇市场、证券市场期货市场和黄金市场等金融市场组成的既有分工又有协作的金融体系。
金融保险业对通信、计算机等电子设备的需求已由单纯的硬件需求转向对软件和服务的需求为了拓展金融服务空间，提高金融交易效率和节约营业成本，金融机构纷纷加大了对电子及通讯设备的投入。在1997年，通信设备、计算机及其他电子设备制造业占金融保险业的中间投入比重高达14.74%，位居同期42部门中第2位。而这一情况在2002年有了新的变化。在2002年，通信设备、计算机及其他电子设备制造业占金融保险业的中间投入只有0.54%，位居同期42部门中第15位。而信息传输、计算机服务和软件业占金融保险业的中间投入却由1997年的3.30%第7位，上升到2002年的10.98%第2位（见上表）。从通信设备、计算机及其他电子设备制造业的角度看，金融保险业已不是它的主要服务对象。因为1997年通信设备、计算机及其他电子设备制造业中间产品的6.28%（第5位）要提供给金融保险业，而在2002年仅为0.52%（第15位）；而信息传输、计算机服务和软件业恰好相反，金融保险业作为它的主要服务对象从年的第7位上升到2002年的第5位（见上表）。上述分析充分说明金融保险业对通信、计算机等电子设备的需求已由单纯的硬件需求转向对软件和服务的需求。
（三）上海金融保险业主要服务产业分析
本部分对直接消耗系数表中金融保险业行向量进行排序，并进一步计算金融保险业在这些产业的中间投入中所占比重和位次。因篇幅所限，这里只在表中展示位于前10名的产业。上述计算可以回答哪个产业是金融保险业的主要服务产业。总结出三点结论：
1.第三产业为金融保险业最重要的服务对象，但地位有所下降。经计算，金融保险业在2002年有56.86%的中间产品提供给第三产业使用，高于提供给第二产业使用的42.25%和第一产业的0.89%。
由此可见第三产业是金融保险业最重要的服务对象
然而相比年第三产业的这一地位有所下降。看表，在1997年最需金融保险业提供服务的10个产业中第三产业占6个，比1997年少2个；更为重要的是，在1997年金融保险业有63.02%的中间产品提供给第三产业，大大高于第二产业的33.78%和第一产业的3.20%。进一步分析，对于2002年金融保险业提供服务最多的6个第三产业，它们对金融保险业也非常依赖。如下表中，2002年金融保险业在6个第三产业的中间投入的比重都较大，位次都居前5名。
2.房地产业、金融保险业、交通运输及仓储业和批发和零售贸易业从1997年到2002年始终是金融保险业的最为主要的服务对象。金融保险业在2002年有11.33%、10.67%、7.74%和7.10%的中间产品提供给房地产业、金融保险业、交通运输及仓储业以及批发和零售贸易业，它们在同期42个部门中高踞前4位，而在1997年的位次分别为第1、4、6和2位。
由此可见这4个产业从1997年到2002年始终是金融保险业的主要服务对象。进一步分析，对于这)4个产业，在2002年金融保险业在它们的中间投入中的比重分别高达)46.51%\35.26%、13.95%和20.60%，位次为第1、1、3和2位。可见金融保险业是这4个产业最为依赖的部门。本文的上述结论与最近几年上海房价的迅速攀升是相一致的；而金融保险业对本部门的依赖也证明了前文所提到的金融协作依存；对交通运输及仓储业和批发和零售贸易业对金融保险业的依赖则是与上海国内金融中心的角色分不开的。
3.金融保险业服务最多的产业恰恰非常需要金融保险业的支持。看表%，在金融保险业提供中间产品最多的10个产业中，金融保险业占它们中间投入的比重虽然差异较大，但有一个共同特点，即比重位次都居于前5位，其中位居第1位、第2位的各有2个产业（它们分别是列第2位的房地产业和金融保险业；列第"位的批发和零售贸易业，石油和天然气开采业），第3位、第5位的各有3个产业。从上面的分析知道，金融保险业占其中间投入的比重越多，其对金融保险业的依赖程度就越高，由此得出金融保险业服务最多的产业恰恰非常需要金融保险业的支持。
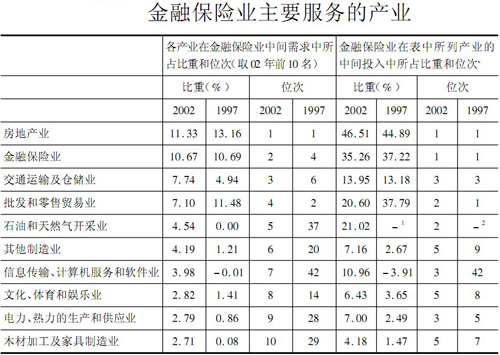
注:1.因为1997年“石油和天然气开采业”的中间投入为0，所以无法计算比重。
2.因为1997年“石油和天然气开采业”的中间投入为0，无法计算比重，所以也就没有位次。
分析描绘了一条以金融保险业为中心的产业链。总体上看，这条产业链的主要组成部分为第三产业，因为第三产业是金融保险业最重要的服务对象，同时第三产业对金融保险业的发展给予了最重要的支持；具体来说，信息传输、计算机服务和软件业、房地产业、交通运输及仓储业以及文化体育和娱乐业与金融保险业相互耗用、相互支撑、息息相关、共同发展；除此之外，金融保险业的发展离不开住宿和餐饮业、卫生社会保障和社会福利业等产业的支持，它们处于这条产业链的上端；同时金融保险业的发展推动了批发和零售贸易业、电力热力的生产和供应业等产业的发展，它们处于产业链的下端。据此，本文提出以下发展上海金融保险业的政策建议：第一，加速金融保险业自身的发展：第二，加快金融信息化建设；第三，加大产业融合的发展力度。
参考文献
投入产出表(部门联系平衡表)，是指以产品部门分类为基础的棋盘式平衡表，用于反映国民经济各部门的投入和产出、投入的来源和产出的去向，以及部门与部门之间相互提供、相互消耗产品的错综复杂的技术经济关系。
投入产出表的产生
投入产出表在二十世纪三十年代产生于美国，它是由美国经济学家、哈佛大学教授瓦西里·列昂惕夫（W.Leontief）在前人关于经济活动相互依存性的研究基础上首先提出并研究和编制的。
列昂惕夫从1931年开始研究投入产出技术，编制投入产出表，目的是研究美国的经济结构。1936年他撰写的“美国经济制度中投入产出数量关系”在《经济学和统计学评论》上发表。它是世界上有关投入产出技术的第一篇论文，标志着投入产出技术的诞生。1953年列昂惕夫与他人合作，出版了《美国经济结构研究》一书。通过这些论著，列昂惕夫提出了投入产出表的概念及其编制方法，阐述了投入产出技术的基本原理，创立了投入产出技术这一科学理论。正是在投入产出技术方面的卓越贡献，列昂惕夫于1973年获得了第五届诺贝尔经济学奖。
投入产出表的发展
投入产出技术从诞生到现在的七十多年里，无论是在理论方面，还是在实践方面都得到了很大的发展，取得了丰硕成果。早期的投入产出模型，只是静态的投入产出模型。后来，随着研究的深入，开发了动态投入产出模型，投入产出技术由静态扩展到动态。近期，随着投入产出技术与数量经济方法等经济分析方法日益融合，投入产出分析应用领域不断扩大。
五十年代末六十年代初，我国经济理论界和一些高等院校的少数同志开始研究投入产出技术，某些高等院校还开设了投入产出技术课程。“文革”期间，此项工作几乎中断。1974年8月，为研究宏观经济发展情况的需要，在国家统计局和国家计委的组织下，由国家统计局、国家计委、中国科学院、中国人民大学、原北京经济学院等单位联合编制了1973年全国61种产品的实物型投入产出表。利用该表开展的应用工作，在制定投资计划和产品生产计划等方面发挥了积极的作用。
十一届三中全会以后，党和国家把工作重点放到经济建设上，这就为包括投入产出技术在内的现代经济分析方法的研究和应用创造条件。从此开始投入产出表的编制工作，投入产出技术的研究和投入产出表的应用工作得到了迅速的发展。
1980年，按照国家统计局的要求，山西省统计局编制了山西省1979年投入产出表，为编制全国投入产出表提供了经验。
1982年，国家统计局、国家计委及有关部门编制了1981年全国投入产出价值表和实物表。
1984年，在1981年全国投入产出价值表的基础上，国家统计局编制了1983年全国投入产出延长表。
1987年，除个别地区外，各省(自治区、直辖市)都编制了本地区投入产出表；一些管理部门还编制厂部门投入产出表；一些企业也编制了企业投入产出表。
1987年3月底，为了适应改革开放的需要，为加强国民经济宏观调控和管理，提高经济决策的科学性，国务院办公厅发出了《关于进行全国投入产出调查的通知》（国办发18号），明确规定每五年（逢二、逢七年份）进行一次全国投入产出调查和编表工作。1987年，我国进行了第一次全国性的投入产出调查和编表工作。《1987年全国投入产出表》的编制成功和在宏观经济调控等方面的成功应用，标志着投入产出技术在我国发展到一个新的阶段。
1992年，国家统计局在1987年全国投入产出表的基础上，编制了1990年投入产出延长表。
1994年和1995年，国家统计局先后编制了1992年全国出价值表和实物表。1992年全国投入产出表为国民经济核算体系全面转轨提供了数据依据。
1996年，国家统计局在1992年全国投入产出表的基础上，编制了1995年全国投入产出延长表。
1999年，国家统计局编制了1997年全国投入产出表。
到目前为止，除西藏以外，全国三十个省(自治区、直辖市)与国家同步编制了1987、1992和1997年本地区投入产出表。部分省(自治区、直辖市)还编制了1990年、1995年和2000年本地区投入产出延长表。今年开始进行第五次全国投入产出调查，并编制2007年全国投入产出表。
投入产出技术不仅在我国宏观和微观经济领域获得了广泛的应用，而且在微观经济领域的应用也取得了可喜的成绩。目前，已有一些企业编制了企业投入产出表，并用于企业计划、生产、成本等管理工作中。
">编辑] 投入产出表的分类按计量单位分：价值型和实物型；按表式结构分：对称型(纯部门)和U-V型(UV表法)；按资料范围分：全国表、地区表和企业表；按时间期限分，静态表和动态表；按考察领域分：产品表，固定资产表、能源表、人口表、教育表、环境污染表，等等。投入产出表基本结构
投入产出表由供给表、使用表和产品部门×产品部门表组成。供给表又称产出表，主栏为n个产品部门，宾栏为m个产业部门，沿行方向看，反映属于某一产品部门的货物或服务是由哪些产业部门生产的，合计为属于该产品部门的货物或服务的总产出；沿列方向看，反映某一产业部门生产各产品部门货物或服务的价值量，合计为该产业部门总产出。全部产业部门总产出等于全部产品部门总产出。通常产品部门个数多于产业部门个数。按生产者价格计算的总供给等于按生产者价格计算的总产出与进口之和；按购买者价格计算的总供给等于按生产者价格计算的总供给与商业和运输费用之和。
使用表又称投入表，通常由三部分组成，第一部分的主栏包括n个产品部门，宾栏包括m个产业部门。沿行方向看，表明各产品部门生产的货物或服务提供给各产业部门使用的价值量，沿列方向看，表明各产业部门从事生产活动所消耗各产品部门生产的货物或服务的价值量；第二部分是第一部分在水平方向上的延伸，其主栏与第一部分相同，也是n个产品部门，其宾栏由最终消费、资本形成总额、出口等最终使用项组成，它反映各产品部门生产的货物或服务用于最终使用的价值量及其构成；第三部分是第一部分在垂直方向上的延伸，其主栏由劳动者报酬、生产税净额、固定资产折旧和营业盈余等增加值项组成，宾栏与第一部分的宾栏一致，也是m个产业部门，它反映各产业部门增加值的构成情况。
产品部门×产品部门表，形式上与使用表相似，也是由三部分组成，第一部分是由名称相同、排列次序相同、数目一致的n个产品部门纵横交叉而成的，其主栏为中间投入、宾栏为中间使用，它充分揭示了国民经济各产品部门之间相互依存、相互制约的技术经济联系，反映了国民经济各部门之间相互依赖、相互提供劳动对象供生产和消耗的过程。沿行方向看，反映第i产品部门生产的货物或服务提供给第j产品部门使用的价值量；沿列方向看，反映第j产品部门在生产过程中消耗第i产品部门生产的货物或服务的价值量。第二部分是第一部分在水平方向上的延伸，其主栏与第一部分的主栏相同，也是n个产品部门；其宾栏由最终消费、资本形成总额、出口等最终使用项组成。它反映各产品部门生产的货物或服务用于各种最终使用的价值量及其构成。第三部分是第一部分在垂直方向上的延伸，其主栏由劳动者报酬、生产税净额、固定资产折旧和营业盈余等增加值项组成；宾栏与第一部分的宾栏相同，也是n个产品部门，它反映各产品部门增加值的构成情况。
产品部门×产品部门表的平衡关系是：
从纵列方向看，第j产品部门中间投入合计＋第j产品部门增加值合计＝第j产品部门总投入
从横行方向看，第i产品部门中间使用合计＋第i产品部门最终使用合计－第i产品部门进口＝第i产品部门总产出
从总量看，总投入＝总产出
第i产品部门总投入＝第i产品部门总产出
中间投入合计＝中间使用合计
投入产出表编制方法
投入产出表的编制方法主要指编制产品部门×产品部门表的方法。产品部门×产品部门表有两种编制方法，一种是间接推导法，另一种是直接分解法。
间接推导法是以产业活动单位为统计单位，按照产业活动单位主产品的性质将其划分到某一产业部门，并编制包括全部产业部门在内的使用表和供给表，然后利用使用表和供给表，依据一定的假定，采用数学方法推导出产品部门×产品部门表的方法。
间接推导法使用的假定有两种，一是产品工艺假定，即假定不管由哪个产业部门生产，同一种产品具有相同的投入结构；二是产业部门工艺假定，即假定同一产业部门不论生产何种产品，都具有相同的投入结构。
直接分解法与间接推导法不同，其统计单位不是产业活动单位，而是一个企业。一个企业，特别是大中型企业，往往同时生产几种、甚至几十种不同质的产品，它们的投入构成不同，根据产品部门的要求，将该企业生产的各种产品，按其性质划归到相应产品部门中，利用企业按产品部门直接分解后的投入构成资料，编制产品部门×产品部门表的方法。
目前我国采用的是以直接分解法为主，间接推导法为辅的编表方法。
">编辑] 投入产出表的四大象限
暂不考虑作为合计数的“总投入”行与“总产出”列以及生产部门的“小计”栏，可将投入产出表划分为四大象限，分别表达特定的经济内容。
（1）第Ⅰ象限(中间产品或中间消耗)：核心。反映各部门之间相互提供、相互消耗产品的技术经济联系。
第Ⅰ象限的特点：
横行标题和纵栏标题是名称、排序相同的产品部门，具有严整的棋盘式结构；横行～提供中间产品的部门(产出部门)；纵栏～消耗中间产品的部门(投入部门)；表中每项数据都具有“产出”与“消耗”的双重涵义。该象限的所有n2 个数据组成“中间流量(中间产品、中间消耗)矩阵”：
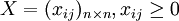
(2)第Ⅱ象限(最终产品或最终使用)：反映各部门提供最终产品的数量和构成情况（可以细分为消费、投资和净出口）。
其数据组成“最终产品列向量”：
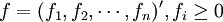
(3)第Ⅲ象限(最初投入或增加值)：反映各部门的最初投入数量及其构成（可以细分）。其数据组成“最初投入(增加值)行向量”：
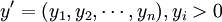
(4)第Ⅳ象限：空白（可在国民核算矩阵中适当开发）。
">编辑] 投入产出表的两个方向
横表：Ⅰ＋Ⅱ，反映各部门的产出及其使用去向，即“产品分配”过程；
竖表：Ⅰ＋Ⅲ，反映各部门的投入及其提供来源，即“价值形成”过程。
“横表”和“竖表”各自存在一定的平衡关系，彼此之间又在总量上相互制约，构成投入产出表建模分析的基础框架。
">编辑] 投入产出表的平衡关系
投入产出表的基本平衡关系有如下三种:
（一）各行(横表)的平衡──产品平衡方程：
中间产品＋最终产品＝总产出
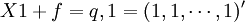
（二）各列(竖表)的平衡──价值平衡方程：
中间投入＋最初投入＝总投入
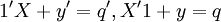
（三）各行列(横表和竖表)的对应平衡：
各部门总产出＝该部门总投入
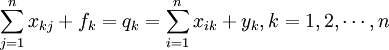
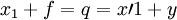
这表明：“产品平衡方程”与“价值平衡方程”既相对独立，又相互制约。
从投入产出表所有行列的角度看，有：
所有部门的总产出＝所有部门的总投入，即:
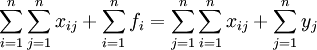
所有部门的中间产品＝所有部门的中间消耗，即:
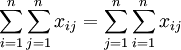
从而有:
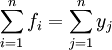
即：所有部门提供的最终产品＝所有部门创造的增加值。
但应注意：
每个部门所提供的中间产品价值与其消耗的中间产品价值通常不等，即：
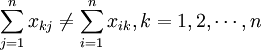
每个部门所提供的最终产品价值与其创造的增加值通常也不等，即：
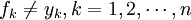
投入产出表的作用
投入产出表可全面系统地反映国民经济各部门之间的投入产出关系，揭示生产过程中各部门之间相互依存和相互制约的经济技术联系。一方面它能告诉人们国民经济各部门的产出情况，以及这些部门的产出是怎样分配给其它部门用于生产或怎样分配给居民和社会用于最终消费或出口到国外的；另一方面它还能告诉人们，各部门为了自身的生产又是怎样从其它部门取得中间投入产品及其最初投入的状况。投入产出核算的功能不仅仅在于反映现各个部门在生产过程中直接的、较为明显的经济技术联系，更重要的是它揭示出各部门之间间接的、较为隐蔽的、甚至被人忽视的经济技术联系。投入产出表为研究产业结构，尤其为制定和检查国民经济计划，研究价格决策，进行各种定量分析提供依据。
投入产出表的主要系数
投入产出系数是进行投入产出分析的重要工具。投入产出系数包括直接消耗系数、完全消耗系数、感应度系数、影响力系数和各种诱发系数。由于直接消耗系数和完全消耗系数是最基本的投入产出系数，这里只介绍直接消耗系数和完全消耗系数的定义和计算方法。
1、直接消耗系数
直接消耗系数，也称为投入系数，记为aij(i,j=1,2,…,n),它是指在生产经营过程中第j产品(或产业)部门的单位总产出所直接消耗的第i产品部门货物或服务的价值量，将各产品(或产业)部门的直接消耗系数用表的形式表现就是直接消耗系数表或直接消耗系数矩阵，通常用字母A表示。
直接消耗系数的计算方法为：用第j产品(或产业)部门的总投入Xj去除该产品部门(或产业)生产经营中所直接消耗的第i产品部门的货物或服务的价值量Xij,用公式表示为:
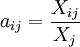(i,j=1,2,…,n)直接消耗系数体现了列昂惕夫模型中生产结构的基本特征，是计算完全消耗系数的基础。它充分揭示了国民经济各部门之间的技术经济联系，即部门之间相互依存和相互制约关系的强弱，并为构造投入产出模型提供了重要的经济参数。
从直接消耗系数的定义和计算方法可以看出，直接消耗系数的取值范围在0≤aij＜1之间，aij越大，说明第j部门对第i部门的直接依赖性越强；aij越小，说明第j部门对第i部门的直接依赖性越弱；aij = 0则说明第j部门对第i部门没有直接的依赖关系。
2、完全消耗系数
完全消耗系数是指第j产品部门每提供一个单位最终使用时，对第i产品部门货物或服务的直接消耗和间接消耗之和。将各产品部门的完全消耗系数用表的形式表现出来，就是完全消耗系数表或完全消耗系数矩阵，通常用字母Ｂ表示。完全消耗系数的计算公式为：
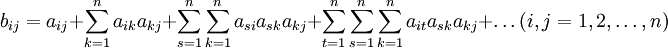
式中的第一项aij表示第j产品部门对第i产品部门的直接消耗量；式中的第二项
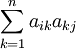表示第j产品部门对第i产品部门的第一轮间接消耗量；式中的第三项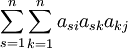为第二轮间接消耗量；式中的第四项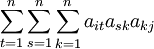为第三轮间接消耗量；依此类推，第n+1项为第n轮间接消耗量。按照公式所示，将直接消耗量和各轮间接消耗量相加就是完全消耗系数。完全消耗系数矩阵可以在直接消耗系数矩阵的基础上计算得到的，利用直接消耗系数矩阵计算完全消耗系数矩阵的公式为：
B = (I − A) − 1 − I
式中的A为直接消耗系数矩阵，I为单位矩阵，为完全消耗系数矩阵。
完全消耗系数，不仅反映了国民经济各部门之间直接的技术经济联系，还反映了国民经济各部门之间间接的技术经济联系，并通过线性关系，将国民经济各部门的总产出与最终使用联系在一起。
基于投入产出表的案例分析 ">编辑] 案例一:基于投入产出表的实证分析
一、计算的理论基础
计算和分析基于投入产出表。投入产出表由三部分组成，按照左上、右上、左下的顺序，分别称为第一、第二和第三象限。其中第一象限反映了一定时期内各产业相互间的供给与需求关系，是投入产出表中最主要的部分。
第一象限的列向量（例如第j列）为产业j的投入结构，即产业j在经济活动中所消耗的其他产业的中间产品值，这反映了产业j的价值形成过程，可揭示产业j对其他产业的拉动程度。利用列向量的值可以计算中间投入率(
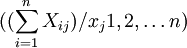,其含义为产业j总产出中消耗其他产业中间产品的比重。中间投入率越高的产业，增加值越低。第一象限的行向量（例如第i行）为产业f的使用结构，即在经济活动中产业i为其他产业提供的中间产品值，可揭示哪些产业是产业i的主要服务对象。利用行向量的值可计算中间需求率
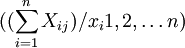,其含义其他产业消耗产业0的中间产品占产业0的总产出的比重。中间需求率越高，对其他产业的推动力或制约性越强。利用公式αij = Xij / xj可将第一象限的数值转化为直接消耗系数矩阵(A),元素αij称为直接消耗系数，其经济含义与上面的分析一致。直接消耗系数矩阵是本文分析的重要基础。
投入产出表是一张平衡表，表中行平衡关系式为：
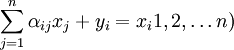(1)其中\alpha_{ij}就为直接消耗系数。
公式(1)表示为矩阵形式为：
AX + Y = X = > X = (I − A) − 1Y (2)
公式(2)中的(I − A) − 1称为里昂剔夫逆矩阵，利用它可以计算产业j感应度系数和影响力系数：。
感应度系数:
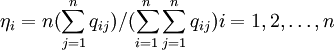。影响力系数:
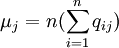
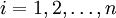
公式中qij是里昂剔夫逆矩阵(I − A) − 1中的第i行第j列的元素。影响力系数反映当产业i每增加一个单位最终使用对其他产业所产生的需求波及程度，其值大于1时，表示产业i的这种需求波及程度高于社会平均水平。感应系数反映每个产业均增加一个单位最终使用时，产业i由此而受到的需求感应程度，其值大于1时，表示产业i所受到的感应程度高于社会平均水平。
二、计算结果及分析
（一）金融保险业在上海各产业中所处的地位分析
金融保险业实现的增加值高，对其他产业的拉动性相对较弱。下表中，上海金融保险业在2002年的中间投入率为39.99%，即金融保险业每实现一单位产出，需要消耗关联产业0.3999单位的中间产品（位列同期42部门的36位，位次较低），同时实现0.6001单位的增加值，实现的增加值是中间投入的1.50倍。
进一步看，金融保险业2002年影响力系数为0.72，即金融保险业每增加%万元最终单位使用时，对其他产业所产生的生产需求为7200元，低于社会平均水平，位列同期42个部门中36名。由此可知金融保险业的增加值高，对其他产业的拉动性相对较弱。需指出，上述两个指标与1997年相比都有所下降。
金融保险业在上海各产业中所处的地位
金融保险业对其他产业的推动性较大，2002年，上海金融保险业的中间投入率为71.40%，即金融保险业总产出的71.40%要作为中间产品提供给关联产业使用，这在同期42个部门中位列21位。进一步，金融保险业2002年感应度系数为%1!3，即其他产业均增加%万元最终使用时，需金融保险业提供的服务产值为1.26万元，高于社会平均水平。从位次来看，这一数值在42个部门中位列5名。这表明金融保险业对其他产业的推动性较大，在经济产业链中处于核心地位。与1997年相比，除中间需求率有所提高外（97年为64.68%），其他都有所下降，这同样表明上海金融保险业近几年发展相对较慢。
总体上看，上海金融保险业对其他产业的拉动性弱，推动力强。拉动性弱主要因为金融保险业是一个高增加值产业；推动力强则表明了金融保险业有着相对重要的产业地位。
（二）上海金融保险业对其他产业的依赖性分析
本部分对直接消耗系数矩阵中金融保险业列向量进行排序，并进一步计算金融保险业在这些产业的中间需求中所占比重和位次，因篇幅所限，这里只在表2中展示位于前10名的产业。上述计算可以反映金融保险业对其他产业的依赖程度。这里总结出三点结论：
金融保险业的发展离不开第三产业的支持。
由表2可知，在金融保险业2002年最为依赖的前10个产业中，第三产业占了8个（前5个产业都为第三产业），比1997年多出3个。经计算，在年金融保险业的中间投入中，第三产业所占比重高达81.64%，高出第二产业4.45倍，由此可见金融保险业的发展离不开第三产业的支持。事实上，金融保险业相比2002年更加需要第三产业的支持，因为不但在年金融保险业最为依赖的个产业中第三产业的个数比年多出3个，更为重要的是，整个金融保险业中间投入中第三产业的占比（81.64%）也要比1997年（62.58%）有大幅度提高。进一步分析，对于年金融保险业最为依赖的个第三产业，金融保险业也是它们的主要服务对象，因为年金融保险业在这个第三产业的中间使用中的比重都较大，从位次上看，除交通运输及仓储业和租赁业和商务服务业外，其他产业的比重、位次都居前名。同样相比年比重和位次都有一定程度的提高，这也与前面的分析相一致（见下表）
金融保险业主要依赖的产业
金融保险业的协作依存程度高。2002年，金融保险业对本部门的直接消耗系数占金融保险业中间投入的比重为35.26%，位居42部门首位，远远高于第二名信息传输、计算机服务和软件业的10.98%，由此可见金融保险业对本部门的依赖性强，协作依存程度高。事实上，从上表中可以看出，这一情况在年就已很明显（比重为，为列首位）。从金融保险业提供中间产品的角度也可得以证明，金融保险业2002年有10.67%的中间产品提供给本部门使用，这一比重仅小于房地产业的11.33%（见上表）。金融保险业的发展是建立在完善金融体系，即众多的金融机构和高效的金融市场之上的。优惠的政策，良好的投资环境和快速健康发展的经济吸引了国内外的众多金融机构，在上海形成了银行、保险公司、证券公司、基金管理公司等多种金融机构以及银行间同业拆借和债券市场、外汇市场、证券市场期货市场和黄金市场等金融市场组成的既有分工又有协作的金融体系。
金融保险业对通信、计算机等电子设备的需求已由单纯的硬件需求转向对软件和服务的需求为了拓展金融服务空间，提高金融交易效率和节约营业成本，金融机构纷纷加大了对电子及通讯设备的投入。在1997年，通信设备、计算机及其他电子设备制造业占金融保险业的中间投入比重高达14.74%，位居同期42部门中第2位。而这一情况在2002年有了新的变化。在2002年，通信设备、计算机及其他电子设备制造业占金融保险业的中间投入只有0.54%，位居同期42部门中第15位。而信息传输、计算机服务和软件业占金融保险业的中间投入却由1997年的3.30%第7位，上升到2002年的10.98%第2位（见上表）。从通信设备、计算机及其他电子设备制造业的角度看，金融保险业已不是它的主要服务对象。因为1997年通信设备、计算机及其他电子设备制造业中间产品的6.28%（第5位）要提供给金融保险业，而在2002年仅为0.52%（第15位）；而信息传输、计算机服务和软件业恰好相反，金融保险业作为它的主要服务对象从年的第7位上升到2002年的第5位（见上表）。上述分析充分说明金融保险业对通信、计算机等电子设备的需求已由单纯的硬件需求转向对软件和服务的需求。
（三）上海金融保险业主要服务产业分析
本部分对直接消耗系数表中金融保险业行向量进行排序，并进一步计算金融保险业在这些产业的中间投入中所占比重和位次。因篇幅所限，这里只在表中展示位于前10名的产业。上述计算可以回答哪个产业是金融保险业的主要服务产业。总结出三点结论：
1.第三产业为金融保险业最重要的服务对象，但地位有所下降。经计算，金融保险业在2002年有56.86%的中间产品提供给第三产业使用，高于提供给第二产业使用的42.25%和第一产业的0.89%。
由此可见第三产业是金融保险业最重要的服务对象
然而相比年第三产业的这一地位有所下降。看表，在1997年最需金融保险业提供服务的10个产业中第三产业占6个，比1997年少2个；更为重要的是，在1997年金融保险业有63.02%的中间产品提供给第三产业，大大高于第二产业的33.78%和第一产业的3.20%。进一步分析，对于2002年金融保险业提供服务最多的6个第三产业，它们对金融保险业也非常依赖。如下表中，2002年金融保险业在6个第三产业的中间投入的比重都较大，位次都居前5名。
2.房地产业、金融保险业、交通运输及仓储业和批发和零售贸易业从1997年到2002年始终是金融保险业的最为主要的服务对象。金融保险业在2002年有11.33%、10.67%、7.74%和7.10%的中间产品提供给房地产业、金融保险业、交通运输及仓储业以及批发和零售贸易业，它们在同期42个部门中高踞前4位，而在1997年的位次分别为第1、4、6和2位。
由此可见这4个产业从1997年到2002年始终是金融保险业的主要服务对象。进一步分析，对于这)4个产业，在2002年金融保险业在它们的中间投入中的比重分别高达)46.51%\35.26%、13.95%和20.60%，位次为第1、1、3和2位。可见金融保险业是这4个产业最为依赖的部门。本文的上述结论与最近几年上海房价的迅速攀升是相一致的；而金融保险业对本部门的依赖也证明了前文所提到的金融协作依存；对交通运输及仓储业和批发和零售贸易业对金融保险业的依赖则是与上海国内金融中心的角色分不开的。
3.金融保险业服务最多的产业恰恰非常需要金融保险业的支持。看表%，在金融保险业提供中间产品最多的10个产业中，金融保险业占它们中间投入的比重虽然差异较大，但有一个共同特点，即比重位次都居于前5位，其中位居第1位、第2位的各有2个产业（它们分别是列第2位的房地产业和金融保险业；列第"位的批发和零售贸易业，石油和天然气开采业），第3位、第5位的各有3个产业。从上面的分析知道，金融保险业占其中间投入的比重越多，其对金融保险业的依赖程度就越高，由此得出金融保险业服务最多的产业恰恰非常需要金融保险业的支持。
注:1.因为1997年“石油和天然气开采业”的中间投入为0，所以无法计算比重。
2.因为1997年“石油和天然气开采业”的中间投入为0，无法计算比重，所以也就没有位次。
分析描绘了一条以金融保险业为中心的产业链。总体上看，这条产业链的主要组成部分为第三产业，因为第三产业是金融保险业最重要的服务对象，同时第三产业对金融保险业的发展给予了最重要的支持；具体来说，信息传输、计算机服务和软件业、房地产业、交通运输及仓储业以及文化体育和娱乐业与金融保险业相互耗用、相互支撑、息息相关、共同发展；除此之外，金融保险业的发展离不开住宿和餐饮业、卫生社会保障和社会福利业等产业的支持，它们处于这条产业链的上端；同时金融保险业的发展推动了批发和零售贸易业、电力热力的生产和供应业等产业的发展，它们处于产业链的下端。据此，本文提出以下发展上海金融保险业的政策建议：第一，加速金融保险业自身的发展：第二，加快金融信息化建设；第三，加大产业融合的发展力度。
参考文献
- ↑ 1.0 1.1 1.2 1.3 1.4 杨灿.《国民经济统计学》第4章 投入产出核算
- ↑ 金德环,田大伟.上海金融保险业的产业关联度研究——基于投入产出表的实证分析.金融与经济.2006(16)
附件列表
词条内容仅供参考，如果您需要解决具体问题
（尤其在法律、医学等领域），建议您咨询相关领域专业人士。