不变权数
什么是不变权数
不变权数是指在一个指数数列中,各个指数的同度量因素(权数)固定不变。
">编辑] 不变权数的应用
不变权数指数在其定基指数和环比指数之间有换算上的方便。即:各环比指数的连乘积等于定基指数;相邻两定基指数相除的商等于环比指数。如欲更改指数基期,可用新定为基期的那年原来的定基指数去除各年原来的定基指数,即得基期更改后各年的定基指数。
现举例说明于下:
表列各环比指数连乘既得相应的定基指数:
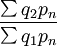 \times\frac{\sum q_3p_n}{\sum q_1p_n}</math>\times\frac{\sum q_1p_n}{\sum q_1p_n}</math>\times\frac{\sum q_5p_n}{\sum q_1p_n}</math>
\times\frac{\sum q_3p_n}{\sum q_1p_n}</math>\times\frac{\sum q_1p_n}{\sum q_1p_n}</math>\times\frac{\sum q_5p_n}{\sum q_1p_n}</math>
相邻两定基指数相除可得相应的环比指数:
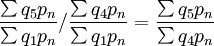
如欲将表列资料改为以第三年为基期。则各年的指数为:
第一年指数为: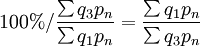
第二年指数: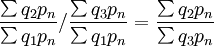
第三年指数: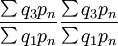 =1或100%
=1或100%
第四年指数: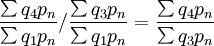
第五年指数: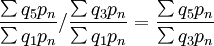
相关条目 可变权数 参考文献
不变权数是指在一个指数数列中,各个指数的同度量因素(权数)固定不变。
">编辑] 不变权数的应用
不变权数指数在其定基指数和环比指数之间有换算上的方便。即:各环比指数的连乘积等于定基指数;相邻两定基指数相除的商等于环比指数。如欲更改指数基期,可用新定为基期的那年原来的定基指数去除各年原来的定基指数,即得基期更改后各年的定基指数。
现举例说明于下:
表列各环比指数连乘既得相应的定基指数:
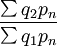 \times\frac{\sum q_3p_n}{\sum q_1p_n}</math>\times\frac{\sum q_1p_n}{\sum q_1p_n}</math>\times\frac{\sum q_5p_n}{\sum q_1p_n}</math>
\times\frac{\sum q_3p_n}{\sum q_1p_n}</math>\times\frac{\sum q_1p_n}{\sum q_1p_n}</math>\times\frac{\sum q_5p_n}{\sum q_1p_n}</math>相邻两定基指数相除可得相应的环比指数:
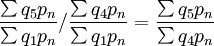
如欲将表列资料改为以第三年为基期。则各年的指数为:
第一年指数为:
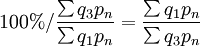
第二年指数:
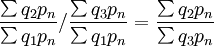
第三年指数:
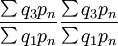 =1或100%
=1或100%第四年指数:
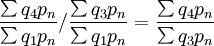
第五年指数:
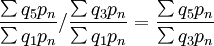
相关条目 可变权数 参考文献
- ↑ 肖彦花.统计学:理论与方法.ISBN:7-81099-221-X/C8.国防科技大学出版社,2005.10.
- ↑ 贾宏宇.统计辞典.ISBN:C8-61.上海人民出版社,1986
附件列表
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
