MLD指数
MLD指数概述
MLD指数(Mean Log Deviation Index)就是当α趋近于0 时所得出的一个熵指数。
MLD指数公式为:

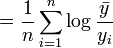
GE(0) 指数不仅符合洛伦茨准则一致性原则,而且可以将人口按组分解成组间差距和组内差距之和,其分解公式为:
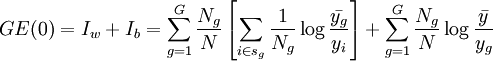
式中n 为在样本中个体的数量,Ng为g组的人口数, 且有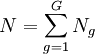 ;
;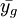 为g 组的人均收入; yi为第i 个样本的收入,参数α代表给予收入分配不同组之间收入的差距的权重。
为g 组的人均收入; yi为第i 个样本的收入,参数α代表给予收入分配不同组之间收入的差距的权重。
参考文献 MLD指数是一个小作品。你可以通过编辑或修订扩充其内容。
MLD指数是一个小作品。你可以通过编辑或修订扩充其内容。
MLD指数(Mean Log Deviation Index)就是当α趋近于0 时所得出的一个熵指数。
MLD指数公式为:

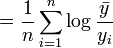
GE(0) 指数不仅符合洛伦茨准则一致性原则,而且可以将人口按组分解成组间差距和组内差距之和,其分解公式为:
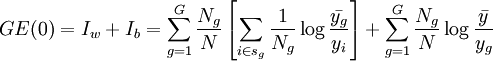
式中n 为在样本中个体的数量,Ng为g组的人口数, 且有
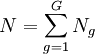 ;
;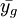 为g 组的人均收入; yi为第i 个样本的收入,参数α代表给予收入分配不同组之间收入的差距的权重。
为g 组的人均收入; yi为第i 个样本的收入,参数α代表给予收入分配不同组之间收入的差距的权重。参考文献
- ↑ 刘志伟.收入分配不公平程度测度方法综述
附件列表
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
如果您认为本词条还有待完善,请 编辑
上一篇 Michaely指数 下一篇 Ross
