回归分析预测法
什么是回归分析预测法?
回归分析预测法,是在分析市场现象自变量和因变量之间相关关系的基础上,建立变量之间的回归方程,并将回归方程作为预测模型,根据自变量在预测期的数量变化来预测因变量关系大多表现为相关关系,因此,回归分析预测法是一种重要的市场预测方法,当我们在对市场现象未来发展状况和水平进行预测时,如果能将影响市场预测对象的主要因素找到,并且能够取得其数量资料,就可以采用回归分析预测法进行预测。它是一种具体的、行之有效的、实用价值很高的常用市场预测方法。
回归分析预测法的分类
回归分析预测法有多种类型。依据相关关系中自变量的个数不同分类,可分为一元回归分析预测法和多元回归分析预测法。在一元回归分析预测法中,自变量只有一个,而在多元回归分析预测法中,自变量有两个以上。依据自变量和因变量之间的相关关系不同,可分为线性回归预测和非线性回归预测。
回归分析预测法的步骤
1.根据预测目标,确定自变量和因变量
明确预测的具体目标,也就确定了因变量。如预测具体目标是下一年度的销售量,那么销售量Y就是因变量。通过市场调查和查阅资料,寻找与预测目标的相关影响因素,即自变量,并从中选出主要的影响因素。
2.建立回归预测模型
依据自变量和因变量的历史统计资料进行计算,在此基础上建立回归分析方程,即回归分析预测模型。
3.进行相关分析
回归分析是对具有因果关系的影响因素(自变量)和预测对象(因变量)所进行的数理统计分析处理。只有当变量与因变量确实存在某种关系时,建立的回归方程才有意义。因此,作为自变量的因素与作为因变量的预测对象是否有关,相关程度如何,以及判断这种相关程度的把握性多大,就成为进行回归分析必须要解决的问题。进行相关分析,一般要求出相关关系,以相关系数的大小来判断自变量和因变量的相关的程度。
4.检验回归预测模型,计算预测误差
回归预测模型是否可用于实际预测,取决于对回归预测模型的检验和对预测误差的计算。回归方程只有通过各种检验,且预测误差较小,才能将回归方程作为预测模型进行预测。
5.计算并确定预测值
利用回归预测模型计算预测值,并对预测值进行综合分析,确定最后的预测值。
应用回归预测法时应注意的问题
应用回归预测法时应首先确定变量之间是否存在相关关系。如果变量之间不存在相关关系,对这些变量应用回归预测法就会得出错误的结果。
正确应用回归分析预测时应注意:
①用定性分析判断现象之间的依存关系;
②避免回归预测的任意外推;
③应用合适的数据资料;
回归分析预测法案例分析 ">编辑] 案例一:回归分析预测法预测新田公司销售
一、新田公司的发展现状
新田公司全称为新田摩托车制造有限公司,成立于1992年3月,当时的锡山市(那时还叫无锡县)有两个生产摩托车的乡镇企业:查桥镇的捷达摩托车厂和洛社镇的雅西摩托车厂。在9l、92年这两家厂可以说是如日中天,但这两家厂又各具特点:雅西摩托车厂完全是自主生产,除发动机外其余配件都由本厂生产;捷达摩托车厂则是装配型厂,配件由其他厂家生产,本厂只是组装(后来也发展成了连发动机都生产的综合型企业)。顾建新当时还只是一家村办企业的供销员,他就瞄准了摩托车行业的发展前景,于是想方设法和捷达厂取得了联系,从1992年3月起为捷达厂生产两种型号的减震器,厂名是无锡减震器厂,由此开始了企业发展的道路。
减震器厂自成立以后,随着捷达摩托车厂摩托车年产量的不断增长而得到了迅速发展。到了1994年6月,顾建新终于有了一个极好的机会:捷达摩托车厂的销售部门和捷达摩托车的销售商产生了予盾,因此捷达摩托车的销售商答应顾建新,若顾建新也能生产出和捷达差不多质量的摩托车,则他们会在相同条件下优先销售顾建新生产的摩托车。有了这个承诺,顾建新于94年lO月就成立了新田摩托车制造有限公司,开始生产新田牌摩托车。
新田公司成立以后,在顾总和匡建中总工程师的领导下,开始了艰苦的创业过程,经过六年多的奋斗,薪田公司终于从一个20多人的小厂发展成了如今的工人总数超过400人,日产摩托车超过200辆,年利润超过2000万的集团型企业,新田摩托车的配件包括发动机在内都由本企业自主生产。
新田公司如今已是一个企业集团,除公司本部(总装厂)外,还有减震器厂、发动机厂、塑件厂、车架车间、油箱车间、喷涂车间等独立部门,这些部门除满足新田公司所需配件外,还可以对外供应。1999年底,由于摩托车市场竞争的日趋激烈,新田公司的销售模式由代理制转向了派员销售制(由公司往各城市直接派出销售人员,负责各城市的销售工作),以减少中间环节,确保公司产品在整个摩托车市场的竞争力。同时,由于销售模式的转变,也带来了生产模式的变化:以前是根据各地代理商的订货量来组织生产,现在则必需根据销售情况和对将来销售情况的预期来组织生产,这给企业的生产组织带来了极大的困难。
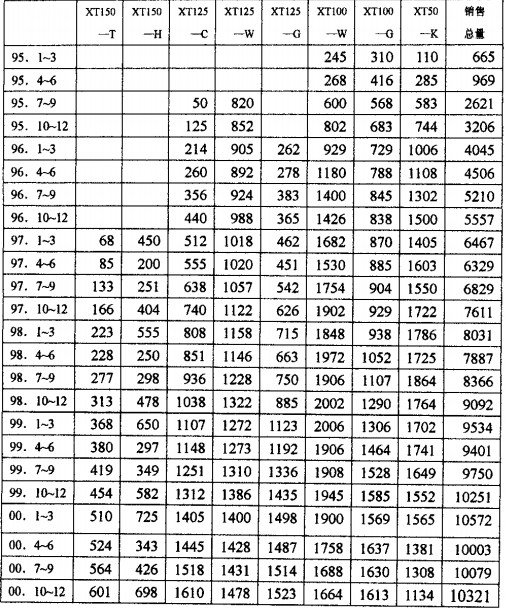
2.新田公司销售的历史数据及要解决的问题新田公司自94年成立以来取得了飞跃性的发展,这可以从新田公司历年的销售数据中看出来。下面所附的表就是新田公司主导产品的销售数据。(参见下面表1.2.3.4)
从表中的数据可以看出,新田公司的生产销售形势还是比较好的,从总体上来说是处于上升趋势,但某些车型的销售也有下降趋势。同时,还有一些问题从销售数据上是看不出来的。自从公司实行派员销售制以来,由于销售的预期值估计不准,常常出现工人加班加点仍赶不上交货对间的情况和工人上了班却无事可做的情况。顾建新总经理和其他公司领导也都发现了这个问题,也找到了原因所在,但由于技术上的原因而无法解决。因此,新田公司目前急需解决的问题就是如何来进行准确可行的销售预测,以保证公司的正常运行。
新田公司2001年第一季度销售数据
新田公司2001年第二季度销售数据
新田公司XT50-M在无锡的销售数据
二、回归分析预测法分析
回归分析预测法是通过研究分析一个应变量对一个或多个自变量的依赖关系,从而通过自变量的已知或设定值来估计和预测应变量均值的一种预测方法。
回归分析预测法又可分成线性回归分析法、非线性回归分析法、虚拟变量回归预测法三种。这三种预测方法在新田公司销售预测中都可以运用。
(一)线性回归分析法的运用
线性回归预测法是指一个或一个以上自变量和应变量之间具有线性关系(一个自变量时为一元线性回归,一个以上自变量时为多元线性回归),配合线性回归模型,根据自变量的变动来预测应变量平均发展趋势的方法。
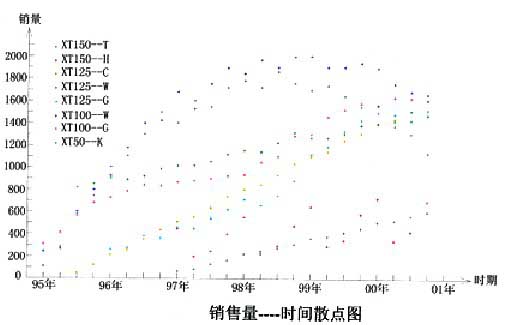
线性回归预测法在销售预测中用得比较多,根据新田公司销售数据的散点圈分析,作者发现新田公司的XTl50~T、XTl25~C XTl25一W三种车型的销售可以用一元线性回归预测法进行预测,由于销售数据是时间性序列,多元线性回归在此不适用。
1.预测模型
由于新田公司销售预测中只用到一元线性回归预测法,而一元线性回归又是一种广泛应用并且比较简单的预测方法,因此,只需对一元线性回归模型作简单介绍。
设X为自变量,Y为应变量,Y与X之间存在某种线性关系,一元线性回归模型为:
yi = a + bxi + εi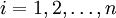 (1)
(1)
式中ε为各种随机因素y的影响总和,ε − (0,σ2);y-N(a+bx,σ2)。则可设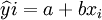 (2)
(2)
对此,可以通过最小二乘法来估计模型的回归系数。根据最小平方原理,必须符合以下条件:
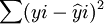 =最小值 (3)
=最小值 (3)
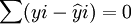 (4)
(4)
根据最小二乘法要求,记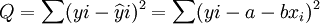
根据极值原理,为使Q具有最小值,可分别对a、b求偏导数,并令其等于零,即
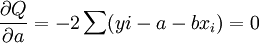
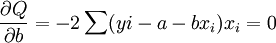
整理的:
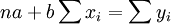
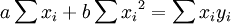
对上两式联立求解,即可得到回归系数的估计值:
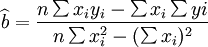 (5)
(5)
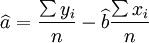 (6)
(6)
相关系数R可根据最小二乘原理及平均数的数学性质得到:
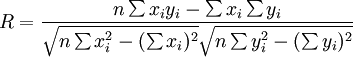 (7)
(7)
相关系数R的绝对值的大小表示相关程度的高低。
①当R=0时,说明是零相关,所求回归系数无效。
②当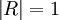 时,说明是完全相关,自变量X与应变量Y之间的关系为函数系。
时,说明是完全相关,自变量X与应变量Y之间的关系为函数系。
⑧当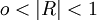 时,说明是部分相关,渊值越大相关程度越高。
时,说明是部分相关,渊值越大相关程度越高。
另外,估计标准差Sy,和预测区间公式参见《预测与决策技术》。
估计标准差: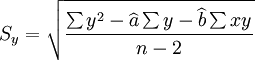 (8)
(8)
预测区间: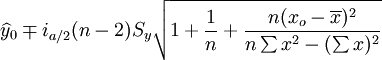 (9)
(9)
在上式中,a为显著水平,n-2为自由度,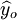 为y在xo的估计值。
为y在xo的估计值。
2.预测计算
根据上面介绍的预测模型,下面就先计算XTl50-T在2001年第一季度的预测销售量。
根据XTl50-T的销售数据有:(X为时间,Y为销售量)。
n=16;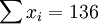 ;
;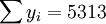 ;
;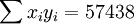 ;
;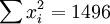 ;
;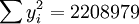
根据公式(5)、(6)、(7)、(8)、(9)有:
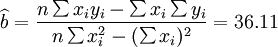
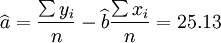
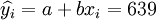 (xi = 17)
(xi = 17)
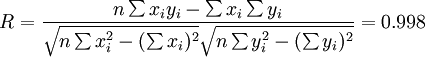
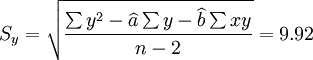
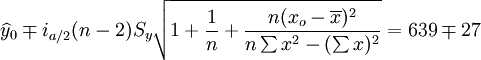
i0.025(14) = 2.145
以上是XT150-T的销售预测计算,同理可计算XT125-C、XT150-W的预测结果,这里不再给出计算过程而直接写出结果:
①XTl25-C的预测结果:
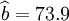 ;
;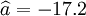 ;
;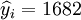 ;R=0.99 ;Sy = 16.56
;R=0.99 ;Sy = 16.56
预测区间为:(1641,1723) (i0.025(20) = 2.086)
②XTl25-W的预测结果:
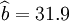 ;
;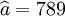 ;
;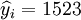 ;R=0.99 ;
;R=0.99 ;
Sy = 29.35
预测区间为:(1450,1596) (i0.025(20) = 2.086)
3.预测结果分析
从上面的预测结果来看,有一点非常奇怪,那就是三种车型的预测中,相关系数R都非常接近于“1”,也就是说,这三种车型的销售量和时间基本上是线性关系,相关程度非常之高。对于这个结果,作者感到很惊讶,为此,特意找到了新田公司,询问这三种车型的销售状况,这才找到了原因。原来,这三种车型是新田公司的形象产品,基本上没有利润,和其他品牌的同类车型相比具有较大的的竞争力,因而这三种车型的销售情况一直很好。公司为了其形象,对这三种车型采取计划供应的方式,按逐年递增的方式供应市场,以使这三种车型一直保持供不应求。由于以上原因,相关系数接近于“1”也就不奇怪了。
另外,作者把通过公式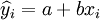 计算得到的各期销售数和实际销售量比较发现,这三种车型有一个共同特点,那就是:第一季度的预测值一般要比实际值大,而第二季度则相反。第三、四季度则预测值和实际值相近。仔细分析原因,可能是因为这三种车型价格都比较高,受年终分配影响,第一季度销量自然较大,随后的第二季度销量就自然偏小。
计算得到的各期销售数和实际销售量比较发现,这三种车型有一个共同特点,那就是:第一季度的预测值一般要比实际值大,而第二季度则相反。第三、四季度则预测值和实际值相近。仔细分析原因,可能是因为这三种车型价格都比较高,受年终分配影响,第一季度销量自然较大,随后的第二季度销量就自然偏小。
对比2001年第一季度的预测值和实际值,以及上面说到的两个特点可以发现,XT150-T的预测结果比较正常,而XTl25-C、XTl25-W的预测值却出现了反而比实际值大的反常情况。通过各期预测值和实际值比较发现,原来XTl25-W从99年第二季度开始就出现预测值大于实际值的情况,根据作者对摩托车市场的了解,认为可能是因为这种车型的销路已经出现问题,不能保持供不应求了。
XTl25-C可能也是这种情况,只不过该车型的滞销出现得稍稍晚而已。通过和新田公司销售部门的联系发现,作者的判断是正确的。
(二)非线性回归预测法的运用
非线性回归预测法是指自变量与因变量之间的关系不是线性的,而是某种非线性关系时的回归预测法。非线性回归预测法的回归模型常见的有以下几种:双曲线模型、二次曲线模型、对数模型、三角函数模型、指数模型、幂函数模型、罗吉斯曲线模型、修正指数增长模型。
通过对新田公司销售数据的散点图分析发现,XT100-W和XT50-K这两种车型的图形接近于抛物线形状,因此可用非线性回归的二次曲线模型来预测。
1.预测模型
非线性回归二次曲线模型为: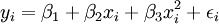 (10)
(10)
令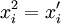 ,则模型变化为:
,则模型变化为: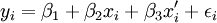 (11)
(11)
上式的矩阵形式为:Y = XB + ε (12)
用最小二乘法作参数估计,可设观察值与模型估计值的残差为E,则
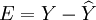 ,
,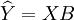
根据小二乘法要求有:
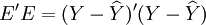 =最小值, (13)
=最小值, (13)
即: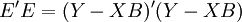 =最小值
=最小值
由极值原理,根据矩阵求导法,对B求导,并令其等于零,得:
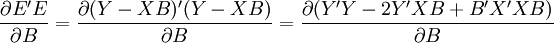
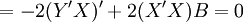
整理得回归系数向量B的估计值为: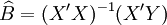 (14)
(14)
二次曲线回归中最常用的检验是R检验和F检验,公式如下:
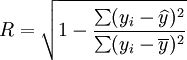 (15)
(15)
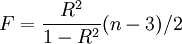 (16)
(16)
在实际工作中,R的计算可用以下简捷公式:
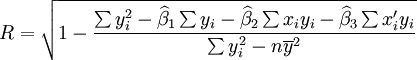 (17)
(17)
估计标准误差为:
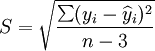 (18)
(18)
预测区间为:
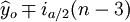 ·S (n<30) (19)
·S (n<30) (19)
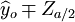 ·S (n>30) (20)
·S (n>30) (20)
2.预测计算
根据上面介绍的预测模型,下面就先进行XT100-W的预测计算。
根据XTl00-W的销售数据及(11)、(14)、(17)、(18)、(19)有(xi为时间变量):
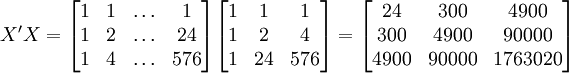
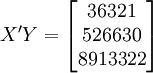 。
。
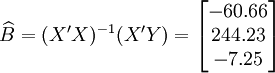
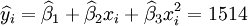 (x_i=25)
(x_i=25)
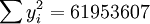 ;
;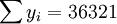 ;
;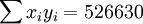 ;
;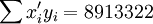
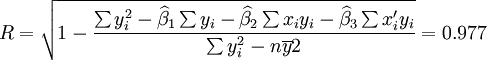
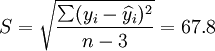
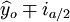 (n-3)·
(n-3)·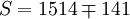 (i0.025(21) = 2.080)
(i0.025(21) = 2.080)
下面再计算XT50-K的预测结果。
根据XT50-K的销售数据及公式(11) 、(14)、(17)、(18)、(19)有:
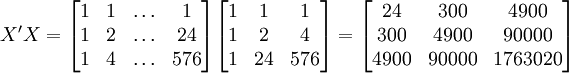 。
。
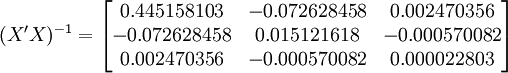
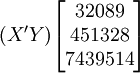
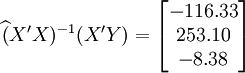
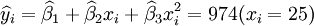
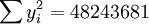 ;
;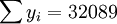 ;
;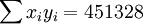 ;
;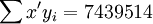
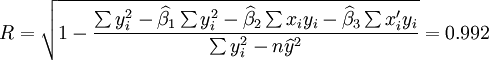
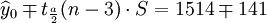 (t0.025(21) = 2.080)
(t0.025(21) = 2.080)
下面再计算XT50—K的预测结果。
根据XT50---K的销售数据及公式(11)、(14)、(17)、(18)、(19)有:
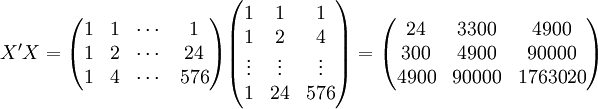
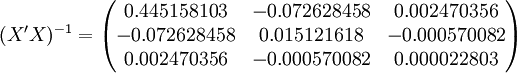
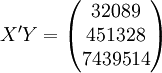
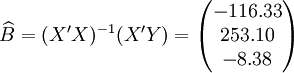
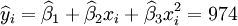 (xi = 25)
(xi = 25)
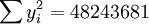 ;
;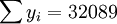 ;
;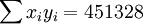 ;
;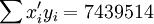
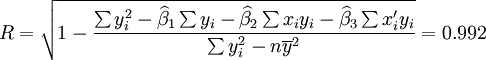
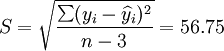
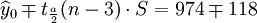 t0.025(21) = 2.080
t0.025(21) = 2.080
3.预测结果分析
从2001年第一季度的预测结果和实际值的比较来看,预测还算是可行的,XTl00—W和XT50—K的实际销售量均在预测范围之内,回归系数也都接近于1,说明这两种车型选取非线性回归的二次曲线模型还是比较合适的。但是,还应该看到,两种车型的预测结果中估计标准差S都比较大,说明回归曲线和实际销售数据的拟合情况并不太好,而S数值的偏大同时也带来了预测范围较大的后果。因此,预测精度较差。
当然了,实际工作中不可能会有真正符合某条曲线的数据存在,只能是从散点图来看大致符合某种曲线,就用该种曲线来进行拟合,以求大致的预测结果。因此,对于XTl00—W和XT50—K的预测还是可行的。
再进一步考虑,XTl00—W的预测值比实际值大了66,说明实际下降趋势比预测的要小,而XT50—K的情况则刚好相反。如果排除偶然因素的话,有可能XTlOO—w销售量的下降趋势在减缓,而XT50—K则相反,下降趋势在加剧。联系实际情况,作者认为是50车型的销量因竞争的日益加剧和政策的影响而加速下滑,而100车型则可能是由于公司的努力而减低了销量下降的速度。作者的这个想法在后来和新田公司总工程师匡建中的交流中得到了验证。
(三)虚拟变量回归预测法的运用
在回归模型分析中,有时还要考虑诸如性别、文化程度、宗教、战争、灾难、季节以及政府经济政策变化等品质变量的影响。这时,可在建立回归模型时将品质变量引入线性回归模型中,这种回归预测法就是虚拟变量回归预测法。
常见的带虚拟变量的回归模型有以下三种形式:
(1)反映政府政策变化或某种因素发生重大变异的跳跃、间断式模型。
(2)具有转折点的系统趋势变化模型。
(3)含有多个虚拟变量的线性回归模型。
虚拟变量回归预测法的适用性一般在散点图上明确看出。在表(1.1)中的数据都不适用。不过,作者发现新田公司的XT50—M在无锡的销售倒是适合用具有转折点的系统趋势变化模型来进行预测。
1.预测模型
由于只有XT50—M在无锡的销售适合用具有转折点的系统趋势变化模型来进行预测(见是表4)下面仅介绍具有转折点的系统趋势变化模型。
具有转折点的系统趋势变化模型为:
yi = β1 + β2xi + β3(xi − x0)Di + εi (21)
式中Di为虚拟变量,Di的取值为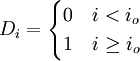
io为发生转折点的时间,xo为io时间xi的观察值。(21)可变形为:
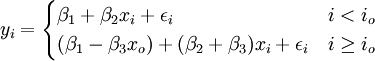
根据(21),可令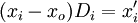 ,,则该虚拟变量回归转化为二元线性回归,可用二元线性回归的计算方法计算。
,,则该虚拟变量回归转化为二元线性回归,可用二元线性回归的计算方法计算。
2)预测计算
经过对散点图观察发现,1998年第四季度为转折点,即i0 = 12,由表(4)的数据及(14)、(17)、(18)、(19)、(21)可得:
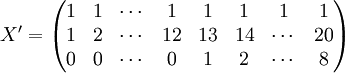
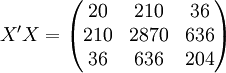
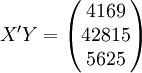
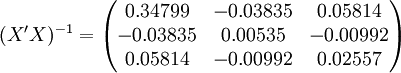
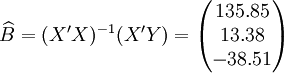
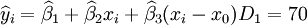 xi = 21
xi = 21
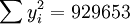 ;
;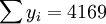 ;
;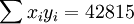 ;
;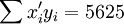
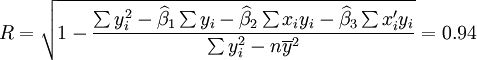
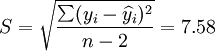
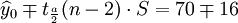 (t0.025(18) = 2.101)
(t0.025(18) = 2.101)
3.预测结果分析
新田公司的XT50—M2001年第一季度在无锡的实际销售量为55辆,和预测结果相比,可以说还在预测范围内,说明该车型在无锡的销售用虚拟变量回归预测法预测还是比较成功的。而之所以会在98年第四季度出现转折点,作者还是了解的,原因就在于98年第四季度无锡市公布了50车型不允许上助力车牌照的规定,从而引起了50车型在无锡的销售量逐步减少。当然了,这种情况销售预测中出现得不多,因此使用也不是很广。
三、回归分析法总结
回归分析预测法是一类比较经典,也比较实用的预测方法。正是由于它经典,因此也就成熟,再加上比较容易理解,运用也就比较广泛。相比之下,其中的线性回归预测法和非线性回归预测法的运用更广些。在实际使用过程中,如果在选择具体的方法和模型时能对数据作较为详细的分析,对散点图的观察分析也能仔细一点的话,预测结果也就会比较令人满意的。当然了回归分析最大的特点就是在偶然中发现必然,而实际情况却常常是千变万化的,有时偶然因素的影响也会超过必然,这时预测结果也就不能很如意,这就要求在预测工作中不能机械,要会灵活运用,要注意了解会影响预测结果的偶然情况,以便对预测结果进行适当修正,这样才能使预测结果更接近实际,也才能使预测能更好地为经济建设服务。从新田公司的回归分析预测结果来看,用线性回归预测法来预测XTl50-T、XTl25—C和XTl25一W都得到了比较满意的结果,而且各项指标也比较好,用虚拟变量回归预测法预测XT50—M也得到了满意的结果。因此可以基本上确定,用上述的预测方法来预测新田公司的这几种车型是可行的。(参见下面二图)。
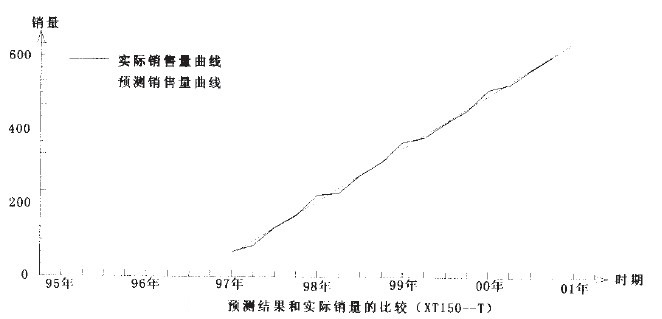
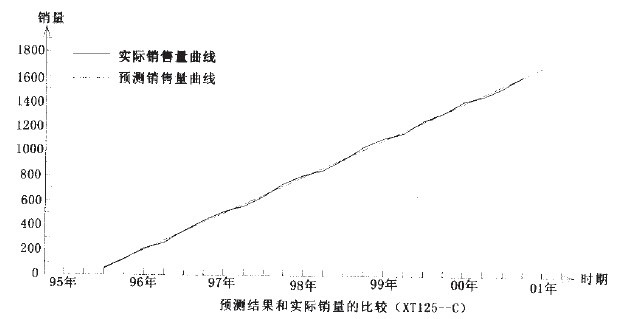
参考文献
回归分析预测法,是在分析市场现象自变量和因变量之间相关关系的基础上,建立变量之间的回归方程,并将回归方程作为预测模型,根据自变量在预测期的数量变化来预测因变量关系大多表现为相关关系,因此,回归分析预测法是一种重要的市场预测方法,当我们在对市场现象未来发展状况和水平进行预测时,如果能将影响市场预测对象的主要因素找到,并且能够取得其数量资料,就可以采用回归分析预测法进行预测。它是一种具体的、行之有效的、实用价值很高的常用市场预测方法。
回归分析预测法的分类
回归分析预测法有多种类型。依据相关关系中自变量的个数不同分类,可分为一元回归分析预测法和多元回归分析预测法。在一元回归分析预测法中,自变量只有一个,而在多元回归分析预测法中,自变量有两个以上。依据自变量和因变量之间的相关关系不同,可分为线性回归预测和非线性回归预测。
回归分析预测法的步骤
1.根据预测目标,确定自变量和因变量
明确预测的具体目标,也就确定了因变量。如预测具体目标是下一年度的销售量,那么销售量Y就是因变量。通过市场调查和查阅资料,寻找与预测目标的相关影响因素,即自变量,并从中选出主要的影响因素。
2.建立回归预测模型
依据自变量和因变量的历史统计资料进行计算,在此基础上建立回归分析方程,即回归分析预测模型。
3.进行相关分析
回归分析是对具有因果关系的影响因素(自变量)和预测对象(因变量)所进行的数理统计分析处理。只有当变量与因变量确实存在某种关系时,建立的回归方程才有意义。因此,作为自变量的因素与作为因变量的预测对象是否有关,相关程度如何,以及判断这种相关程度的把握性多大,就成为进行回归分析必须要解决的问题。进行相关分析,一般要求出相关关系,以相关系数的大小来判断自变量和因变量的相关的程度。
4.检验回归预测模型,计算预测误差
回归预测模型是否可用于实际预测,取决于对回归预测模型的检验和对预测误差的计算。回归方程只有通过各种检验,且预测误差较小,才能将回归方程作为预测模型进行预测。
5.计算并确定预测值
利用回归预测模型计算预测值,并对预测值进行综合分析,确定最后的预测值。
应用回归预测法时应注意的问题
应用回归预测法时应首先确定变量之间是否存在相关关系。如果变量之间不存在相关关系,对这些变量应用回归预测法就会得出错误的结果。
正确应用回归分析预测时应注意:
①用定性分析判断现象之间的依存关系;
②避免回归预测的任意外推;
③应用合适的数据资料;
回归分析预测法案例分析 ">编辑] 案例一:回归分析预测法预测新田公司销售
一、新田公司的发展现状
新田公司全称为新田摩托车制造有限公司,成立于1992年3月,当时的锡山市(那时还叫无锡县)有两个生产摩托车的乡镇企业:查桥镇的捷达摩托车厂和洛社镇的雅西摩托车厂。在9l、92年这两家厂可以说是如日中天,但这两家厂又各具特点:雅西摩托车厂完全是自主生产,除发动机外其余配件都由本厂生产;捷达摩托车厂则是装配型厂,配件由其他厂家生产,本厂只是组装(后来也发展成了连发动机都生产的综合型企业)。顾建新当时还只是一家村办企业的供销员,他就瞄准了摩托车行业的发展前景,于是想方设法和捷达厂取得了联系,从1992年3月起为捷达厂生产两种型号的减震器,厂名是无锡减震器厂,由此开始了企业发展的道路。
减震器厂自成立以后,随着捷达摩托车厂摩托车年产量的不断增长而得到了迅速发展。到了1994年6月,顾建新终于有了一个极好的机会:捷达摩托车厂的销售部门和捷达摩托车的销售商产生了予盾,因此捷达摩托车的销售商答应顾建新,若顾建新也能生产出和捷达差不多质量的摩托车,则他们会在相同条件下优先销售顾建新生产的摩托车。有了这个承诺,顾建新于94年lO月就成立了新田摩托车制造有限公司,开始生产新田牌摩托车。
新田公司成立以后,在顾总和匡建中总工程师的领导下,开始了艰苦的创业过程,经过六年多的奋斗,薪田公司终于从一个20多人的小厂发展成了如今的工人总数超过400人,日产摩托车超过200辆,年利润超过2000万的集团型企业,新田摩托车的配件包括发动机在内都由本企业自主生产。
新田公司如今已是一个企业集团,除公司本部(总装厂)外,还有减震器厂、发动机厂、塑件厂、车架车间、油箱车间、喷涂车间等独立部门,这些部门除满足新田公司所需配件外,还可以对外供应。1999年底,由于摩托车市场竞争的日趋激烈,新田公司的销售模式由代理制转向了派员销售制(由公司往各城市直接派出销售人员,负责各城市的销售工作),以减少中间环节,确保公司产品在整个摩托车市场的竞争力。同时,由于销售模式的转变,也带来了生产模式的变化:以前是根据各地代理商的订货量来组织生产,现在则必需根据销售情况和对将来销售情况的预期来组织生产,这给企业的生产组织带来了极大的困难。
2.新田公司销售的历史数据及要解决的问题新田公司自94年成立以来取得了飞跃性的发展,这可以从新田公司历年的销售数据中看出来。下面所附的表就是新田公司主导产品的销售数据。(参见下面表1.2.3.4)
从表中的数据可以看出,新田公司的生产销售形势还是比较好的,从总体上来说是处于上升趋势,但某些车型的销售也有下降趋势。同时,还有一些问题从销售数据上是看不出来的。自从公司实行派员销售制以来,由于销售的预期值估计不准,常常出现工人加班加点仍赶不上交货对间的情况和工人上了班却无事可做的情况。顾建新总经理和其他公司领导也都发现了这个问题,也找到了原因所在,但由于技术上的原因而无法解决。因此,新田公司目前急需解决的问题就是如何来进行准确可行的销售预测,以保证公司的正常运行。

新田公司2001年第一季度销售数据
新田公司2001年第二季度销售数据
新田公司XT50-M在无锡的销售数据

二、回归分析预测法分析
回归分析预测法是通过研究分析一个应变量对一个或多个自变量的依赖关系,从而通过自变量的已知或设定值来估计和预测应变量均值的一种预测方法。
回归分析预测法又可分成线性回归分析法、非线性回归分析法、虚拟变量回归预测法三种。这三种预测方法在新田公司销售预测中都可以运用。
(一)线性回归分析法的运用
线性回归预测法是指一个或一个以上自变量和应变量之间具有线性关系(一个自变量时为一元线性回归,一个以上自变量时为多元线性回归),配合线性回归模型,根据自变量的变动来预测应变量平均发展趋势的方法。
线性回归预测法在销售预测中用得比较多,根据新田公司销售数据的散点圈分析,作者发现新田公司的XTl50~T、XTl25~C XTl25一W三种车型的销售可以用一元线性回归预测法进行预测,由于销售数据是时间性序列,多元线性回归在此不适用。
1.预测模型
由于新田公司销售预测中只用到一元线性回归预测法,而一元线性回归又是一种广泛应用并且比较简单的预测方法,因此,只需对一元线性回归模型作简单介绍。
设X为自变量,Y为应变量,Y与X之间存在某种线性关系,一元线性回归模型为:
yi = a + bxi + εi
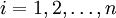 (1)
(1)式中ε为各种随机因素y的影响总和,ε − (0,σ2);y-N(a+bx,σ2)。则可设
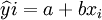 (2)
(2)对此,可以通过最小二乘法来估计模型的回归系数。根据最小平方原理,必须符合以下条件:
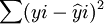 =最小值 (3)
=最小值 (3)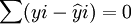 (4)
(4)根据最小二乘法要求,记
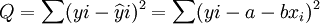
根据极值原理,为使Q具有最小值,可分别对a、b求偏导数,并令其等于零,即
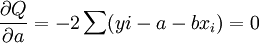
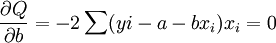
整理的:
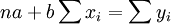
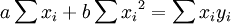
对上两式联立求解,即可得到回归系数的估计值:
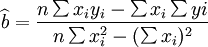 (5)
(5)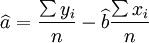 (6)
(6)相关系数R可根据最小二乘原理及平均数的数学性质得到:
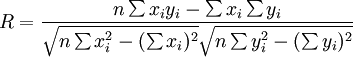 (7)
(7)相关系数R的绝对值的大小表示相关程度的高低。
①当R=0时,说明是零相关,所求回归系数无效。
②当
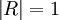 时,说明是完全相关,自变量X与应变量Y之间的关系为函数系。
时,说明是完全相关,自变量X与应变量Y之间的关系为函数系。⑧当
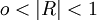 时,说明是部分相关,渊值越大相关程度越高。
时,说明是部分相关,渊值越大相关程度越高。另外,估计标准差Sy,和预测区间公式参见《预测与决策技术》。
估计标准差:
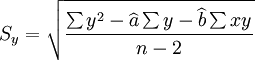 (8)
(8)预测区间:
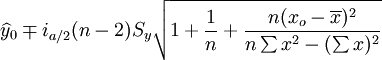 (9)
(9)在上式中,a为显著水平,n-2为自由度,
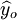 为y在xo的估计值。
为y在xo的估计值。2.预测计算
根据上面介绍的预测模型,下面就先计算XTl50-T在2001年第一季度的预测销售量。
根据XTl50-T的销售数据有:(X为时间,Y为销售量)。
n=16;
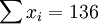 ;
;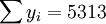 ;
;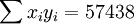 ;
;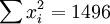 ;
;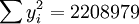
根据公式(5)、(6)、(7)、(8)、(9)有:
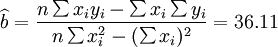
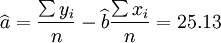
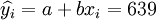 (xi = 17)
(xi = 17)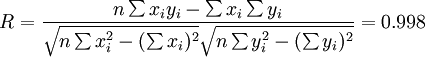
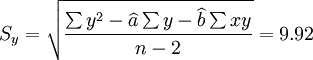
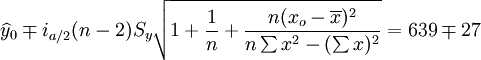
i0.025(14) = 2.145
以上是XT150-T的销售预测计算,同理可计算XT125-C、XT150-W的预测结果,这里不再给出计算过程而直接写出结果:
①XTl25-C的预测结果:
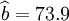 ;
;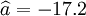 ;
;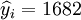 ;R=0.99 ;Sy = 16.56
;R=0.99 ;Sy = 16.56预测区间为:(1641,1723) (i0.025(20) = 2.086)
②XTl25-W的预测结果:
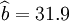 ;
;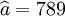 ;
;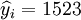 ;R=0.99 ;
;R=0.99 ;Sy = 29.35
预测区间为:(1450,1596) (i0.025(20) = 2.086)
3.预测结果分析
从上面的预测结果来看,有一点非常奇怪,那就是三种车型的预测中,相关系数R都非常接近于“1”,也就是说,这三种车型的销售量和时间基本上是线性关系,相关程度非常之高。对于这个结果,作者感到很惊讶,为此,特意找到了新田公司,询问这三种车型的销售状况,这才找到了原因。原来,这三种车型是新田公司的形象产品,基本上没有利润,和其他品牌的同类车型相比具有较大的的竞争力,因而这三种车型的销售情况一直很好。公司为了其形象,对这三种车型采取计划供应的方式,按逐年递增的方式供应市场,以使这三种车型一直保持供不应求。由于以上原因,相关系数接近于“1”也就不奇怪了。
另外,作者把通过公式
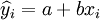 计算得到的各期销售数和实际销售量比较发现,这三种车型有一个共同特点,那就是:第一季度的预测值一般要比实际值大,而第二季度则相反。第三、四季度则预测值和实际值相近。仔细分析原因,可能是因为这三种车型价格都比较高,受年终分配影响,第一季度销量自然较大,随后的第二季度销量就自然偏小。
计算得到的各期销售数和实际销售量比较发现,这三种车型有一个共同特点,那就是:第一季度的预测值一般要比实际值大,而第二季度则相反。第三、四季度则预测值和实际值相近。仔细分析原因,可能是因为这三种车型价格都比较高,受年终分配影响,第一季度销量自然较大,随后的第二季度销量就自然偏小。对比2001年第一季度的预测值和实际值,以及上面说到的两个特点可以发现,XT150-T的预测结果比较正常,而XTl25-C、XTl25-W的预测值却出现了反而比实际值大的反常情况。通过各期预测值和实际值比较发现,原来XTl25-W从99年第二季度开始就出现预测值大于实际值的情况,根据作者对摩托车市场的了解,认为可能是因为这种车型的销路已经出现问题,不能保持供不应求了。
XTl25-C可能也是这种情况,只不过该车型的滞销出现得稍稍晚而已。通过和新田公司销售部门的联系发现,作者的判断是正确的。
(二)非线性回归预测法的运用
非线性回归预测法是指自变量与因变量之间的关系不是线性的,而是某种非线性关系时的回归预测法。非线性回归预测法的回归模型常见的有以下几种:双曲线模型、二次曲线模型、对数模型、三角函数模型、指数模型、幂函数模型、罗吉斯曲线模型、修正指数增长模型。
通过对新田公司销售数据的散点图分析发现,XT100-W和XT50-K这两种车型的图形接近于抛物线形状,因此可用非线性回归的二次曲线模型来预测。
1.预测模型
非线性回归二次曲线模型为:
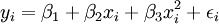 (10)
(10)令
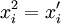 ,则模型变化为:
,则模型变化为: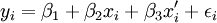 (11)
(11)上式的矩阵形式为:Y = XB + ε (12)
用最小二乘法作参数估计,可设观察值与模型估计值的残差为E,则
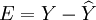 ,
,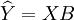
根据小二乘法要求有:
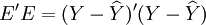 =最小值, (13)
=最小值, (13)即:
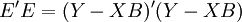 =最小值
=最小值由极值原理,根据矩阵求导法,对B求导,并令其等于零,得:
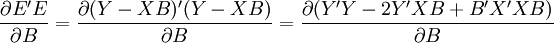
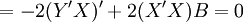
整理得回归系数向量B的估计值为:
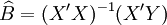 (14)
(14)二次曲线回归中最常用的检验是R检验和F检验,公式如下:
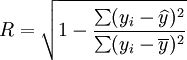 (15)
(15)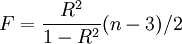 (16)
(16)在实际工作中,R的计算可用以下简捷公式:
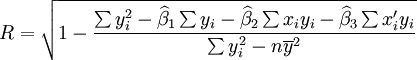 (17)
(17)估计标准误差为:
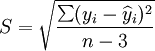 (18)
(18)预测区间为:
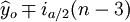 ·S (n<30) (19)
·S (n<30) (19)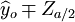 ·S (n>30) (20)
·S (n>30) (20)2.预测计算
根据上面介绍的预测模型,下面就先进行XT100-W的预测计算。
根据XTl00-W的销售数据及(11)、(14)、(17)、(18)、(19)有(xi为时间变量):
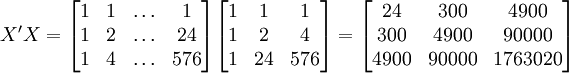
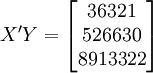 。
。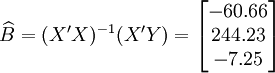
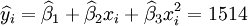 (x_i=25)
(x_i=25)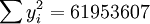 ;
;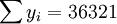 ;
;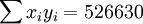 ;
;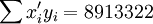
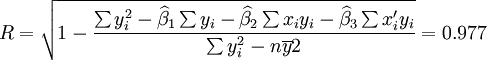
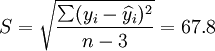
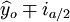 (n-3)·
(n-3)·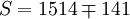 (i0.025(21) = 2.080)
(i0.025(21) = 2.080)下面再计算XT50-K的预测结果。
根据XT50-K的销售数据及公式(11) 、(14)、(17)、(18)、(19)有:
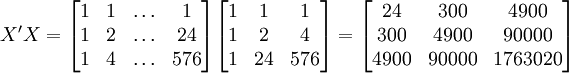 。
。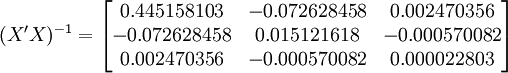
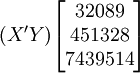
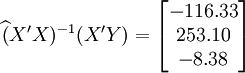
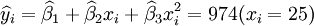
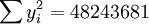 ;
;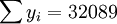 ;
;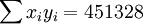 ;
;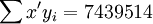
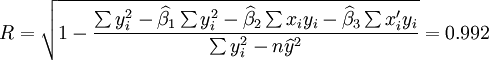
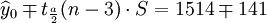 (t0.025(21) = 2.080)
(t0.025(21) = 2.080)下面再计算XT50—K的预测结果。
根据XT50---K的销售数据及公式(11)、(14)、(17)、(18)、(19)有:
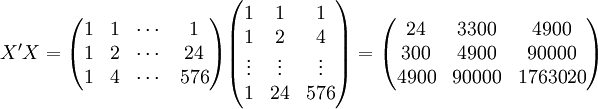
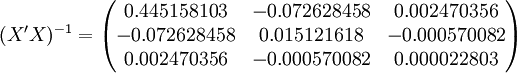
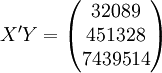
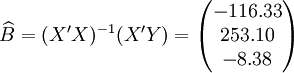
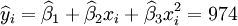 (xi = 25)
(xi = 25)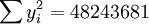 ;
;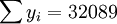 ;
;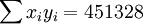 ;
;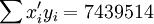
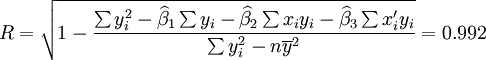
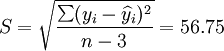
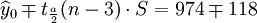 t0.025(21) = 2.080
t0.025(21) = 2.0803.预测结果分析
从2001年第一季度的预测结果和实际值的比较来看,预测还算是可行的,XTl00—W和XT50—K的实际销售量均在预测范围之内,回归系数也都接近于1,说明这两种车型选取非线性回归的二次曲线模型还是比较合适的。但是,还应该看到,两种车型的预测结果中估计标准差S都比较大,说明回归曲线和实际销售数据的拟合情况并不太好,而S数值的偏大同时也带来了预测范围较大的后果。因此,预测精度较差。
当然了,实际工作中不可能会有真正符合某条曲线的数据存在,只能是从散点图来看大致符合某种曲线,就用该种曲线来进行拟合,以求大致的预测结果。因此,对于XTl00—W和XT50—K的预测还是可行的。
再进一步考虑,XTl00—W的预测值比实际值大了66,说明实际下降趋势比预测的要小,而XT50—K的情况则刚好相反。如果排除偶然因素的话,有可能XTlOO—w销售量的下降趋势在减缓,而XT50—K则相反,下降趋势在加剧。联系实际情况,作者认为是50车型的销量因竞争的日益加剧和政策的影响而加速下滑,而100车型则可能是由于公司的努力而减低了销量下降的速度。作者的这个想法在后来和新田公司总工程师匡建中的交流中得到了验证。
(三)虚拟变量回归预测法的运用
在回归模型分析中,有时还要考虑诸如性别、文化程度、宗教、战争、灾难、季节以及政府经济政策变化等品质变量的影响。这时,可在建立回归模型时将品质变量引入线性回归模型中,这种回归预测法就是虚拟变量回归预测法。
常见的带虚拟变量的回归模型有以下三种形式:
(1)反映政府政策变化或某种因素发生重大变异的跳跃、间断式模型。
(2)具有转折点的系统趋势变化模型。
(3)含有多个虚拟变量的线性回归模型。
虚拟变量回归预测法的适用性一般在散点图上明确看出。在表(1.1)中的数据都不适用。不过,作者发现新田公司的XT50—M在无锡的销售倒是适合用具有转折点的系统趋势变化模型来进行预测。
1.预测模型
由于只有XT50—M在无锡的销售适合用具有转折点的系统趋势变化模型来进行预测(见是表4)下面仅介绍具有转折点的系统趋势变化模型。
具有转折点的系统趋势变化模型为:
yi = β1 + β2xi + β3(xi − x0)Di + εi (21)
式中Di为虚拟变量,Di的取值为
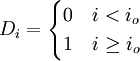
io为发生转折点的时间,xo为io时间xi的观察值。(21)可变形为:
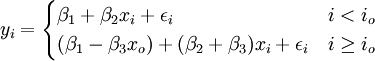
根据(21),可令
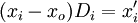 ,,则该虚拟变量回归转化为二元线性回归,可用二元线性回归的计算方法计算。
,,则该虚拟变量回归转化为二元线性回归,可用二元线性回归的计算方法计算。2)预测计算
经过对散点图观察发现,1998年第四季度为转折点,即i0 = 12,由表(4)的数据及(14)、(17)、(18)、(19)、(21)可得:
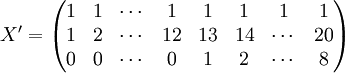
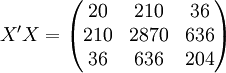
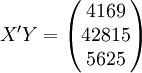
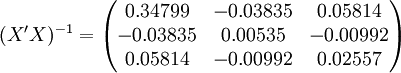
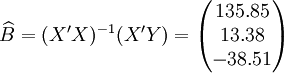
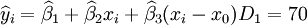 xi = 21
xi = 21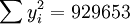 ;
;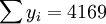 ;
;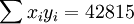 ;
;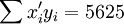
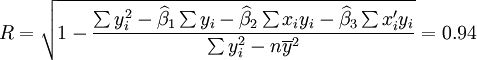
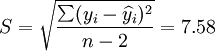
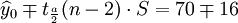 (t0.025(18) = 2.101)
(t0.025(18) = 2.101)3.预测结果分析
新田公司的XT50—M2001年第一季度在无锡的实际销售量为55辆,和预测结果相比,可以说还在预测范围内,说明该车型在无锡的销售用虚拟变量回归预测法预测还是比较成功的。而之所以会在98年第四季度出现转折点,作者还是了解的,原因就在于98年第四季度无锡市公布了50车型不允许上助力车牌照的规定,从而引起了50车型在无锡的销售量逐步减少。当然了,这种情况销售预测中出现得不多,因此使用也不是很广。
三、回归分析法总结
回归分析预测法是一类比较经典,也比较实用的预测方法。正是由于它经典,因此也就成熟,再加上比较容易理解,运用也就比较广泛。相比之下,其中的线性回归预测法和非线性回归预测法的运用更广些。在实际使用过程中,如果在选择具体的方法和模型时能对数据作较为详细的分析,对散点图的观察分析也能仔细一点的话,预测结果也就会比较令人满意的。当然了回归分析最大的特点就是在偶然中发现必然,而实际情况却常常是千变万化的,有时偶然因素的影响也会超过必然,这时预测结果也就不能很如意,这就要求在预测工作中不能机械,要会灵活运用,要注意了解会影响预测结果的偶然情况,以便对预测结果进行适当修正,这样才能使预测结果更接近实际,也才能使预测能更好地为经济建设服务。从新田公司的回归分析预测结果来看,用线性回归预测法来预测XTl50-T、XTl25—C和XTl25一W都得到了比较满意的结果,而且各项指标也比较好,用虚拟变量回归预测法预测XT50—M也得到了满意的结果。因此可以基本上确定,用上述的预测方法来预测新田公司的这几种车型是可行的。(参见下面二图)。


参考文献
- ↑ 钱晓星.新田公司摩托车销售预测研究.2002
附件列表
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
