斯塔克尔伯格模型
什么是斯塔克尔伯格模型?
斯塔克尔伯格模型由德国经济学家斯塔克尔伯格(H. Von Stackelberg)在上世纪30年代提出。
在古诺模型和伯特兰德模型里,竞争厂商在市场上的地位是平等的,因而它们的行为是相似的。而且,它们的决策是同时的。当企业甲在作决策时,它并不知道企业乙的决策。但事实上,在有些市场,竞争厂商之间的地位并不是对称的,市场地位的不对称引起了决策次序的不对称,通常,小企业先观察到大企业的行为,再决定自己的对策。德国经济学家斯塔克尔伯格建立的模型就反映了这种不对称的竞争。
该模型的假定是:主导企业知道跟随企业一定会对它的产量作出反应,因而当它在确定产量时,把跟随企业力反应也考虑进去了。因此这个模型也被称为“主导企业模型”。
斯塔克尔伯格模型假设条件
假设厂商1先决定它的产量,然后厂商2知道厂商1的产量后再作出它的产量决策。
因此,在确定自己产量时,厂商1必须考虑厂商2将如何作出反应。
其他假设与古诺模型相同,
斯塔克尔伯格模型分析
斯塔克尔伯格模型是一个价格领导模型,厂商之间存在着行动次序的区别。产量的决定依据以下次序:领导性厂商决定一个产量,然后跟随着厂商可以观察到这个产量,然后根据领导性厂商的产量来决定他自己的产量。需要注意的是,领导性厂商在决定自己的产量的时候,充分了解跟随厂商会如何行动——这意味着领导性厂商可以知道跟随厂商的反应函数。因此,领导性厂商自然会预期到自己决定的产量对跟随厂商的影响。正是在考虑到这种影响的情况下,领导性厂商所决定的产量将是一个以跟随厂商的反应函数为约束的利润最大化产量。在斯塔克尔伯格模型中,领导性厂商的决策不再需要自己的反应函数。
斯塔克尔伯格模型案例分析 ">编辑]案例一:基于斯塔克尔伯格模型的环渤海港口竞争机制分析
一、斯塔克尔伯格港口竞争机制模型
这里所说的港口竞争指的是同一港口群内不同港口之间的竞争。一个区域内往往形成一个港口群,群内港口面临共同的陆向或者海向腹地,因而竞争激烈。港口服务的提供需要具备临海的地理位置,且港口投资的成本大,这些条件的存在限制了港口产业中港口的数量,使得进入港口的产业进入壁垒较大,因而也就决定了港口产业的市场结构。
假设在开始阶段,某区域只有一个港口1,其内陆腹地流出或流向该腹地的所有产品均通过港口1,那么港口1完全垄断市场。假设不存在进入成本,即新港口以任意规模的投资进入均可获得收益,于是潜在进入者港口2可以以任意规模进入市场,并获得利润。下面基于斯塔克尔伯格模型,从产量方面说明港口之间的竞争。
斯塔克尔伯格模型用来描述一个充当领导者角色的厂商与作为追随者的厂商之间的相互影响。假设在所有的港口中存在一个在该行业中处于支配地位的港口,该处于支配地位的港口是斯塔克尔伯格领导者。斯塔克尔伯格领导者对产量的选择将直接导致市场价格的变化,从而影响其他追随者改变自己的产量。同样,处于支配地位的港口产量(对其货物、集装箱的吞吐量的选择)发生变化,供给的变化导致市场价格(港口货物、集装箱装卸、航运价格、泊位费用等费用)变化,而市场价格的变化又促使其他港口改变各自的产量,以保持利润最大化。港口之间博弈的主体是能决定港口产量的政府或者企业。假设条件如下:
1.有两个港口1、2,港口1是产量领导者,产量为y1,港口2是跟随者,即根据港口1的选择而选择产量y2。市场价格是总产量的函数,即p = f(y1 + y2);反需求函数可以认为是p = a − b(y1 + y2)。
2.港口1、2均根据自己的产量确定最大化利润,且两个港口的边际成本为0。
3.由于港口1在整个行业处于支配地位,港口2将在港口1产量确定的情况下实现利润最大化,而港口1也知道港口2根据自己产量确定它的产量,即完全信息。
4.港口2根据港口1确定产量,对港口2而言,港口1的产量是常量,港口1在选择产量时也会考虑到其对港口2的影响。
由于其成本假设为0,港口2的利润函数为:
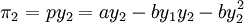 ,
,
利润最大化的条件: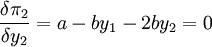 ,
,
所以,求得反应函数: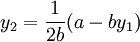
将上面的反应函数代入港口1的利润函数:
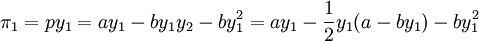
其利润最大化条件: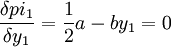
所以均衡时港口1最大利润化的产量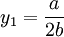
那么,同理可以求出港口2最大利润化的产量: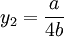
在斯塔克尔伯格模型下均衡时两个港口的产量分别为: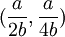 此时港口1、港口2的收益分别为:
此时港口1、港口2的收益分别为:
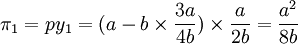
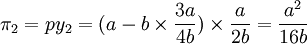
这样,在港口1的产量领导下,港口1和港口2实
现了短期的均衡,均衡时的产量为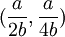 ,市场价格
,市场价格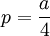 。港口1获得的利润大于港口2的利润,说明了先动者的优势,并且,港口1通过产量的选择限制了港口2的进入规模。
。港口1获得的利润大于港口2的利润,说明了先动者的优势,并且,港口1通过产量的选择限制了港口2的进入规模。
二、斯塔克尔伯格港口竞争机制模型的扩展
我们定义港口产量是港口投入资本量的函数,存在下列函数关系:Y=f(K),其反函数K = f − 1(Y)代表港口产量的多少取决于它的资本存量多少。事实上,进入港口行业需要大量的投资,其沉没成本很大,需要较大的进入成本。所以,把进入成本F引入模型,在规模收益递增的情况下,小规模的进入不能获得利润。正是因为进入成本大,才使在位者港口可以遏制其他竞争者的进入。
在进入成本存在的情况下,港口2进入市场后的利润函数变为:
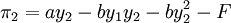
那么,在位者港口1通过制定产量Y1,使得港口2的最大利润满足maxπ2 = 0,这样港口2因进入市场无利可图而不进入,港口1通过产量的选择阻止港口2进入,阻止进人的产量水平由下式确定:
max(ay2 − by1y2 − by − 22 − F)
港口2取得最大利润的条件:
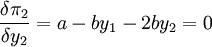
所以,当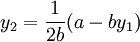 时,港口2的利润最大,最大利润为:
时,港口2的利润最大,最大利润为:
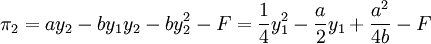
港口1选择自己的产量y1,使港口2的利润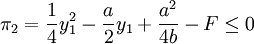
若式子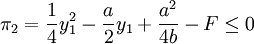 ,即满足
,即满足
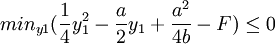
y1 = a时,上式有最小值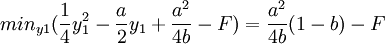
所以,当满足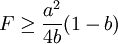 时,港口2利润
时,港口2利润 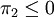
下面分别对几种情况进行讨论:
1. 当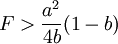 时,
时,
y1的取值范围满足 时,π2 < O;
时,π2 < O;
y1取其他值时,π2 > O。
2. 当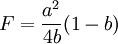 时,y1 = a时,π2 = 0;
时,y1 = a时,π2 = 0;
y1取其他值时,π2 > 0。
3. 当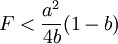 时,π2 > 0。此时,进入壁垒较小,因而不管港口1怎样调整自己的产量,都不能阻止港口2进入市场。
时,π2 > 0。此时,进入壁垒较小,因而不管港口1怎样调整自己的产量,都不能阻止港口2进入市场。
由上面的模型可以说明港口之间的竞争机制:在位者根据竞争者进入成本的大小选择遏止其进入还是默许进入策略;而竞争者或者潜在进入者却只能根据其进入成本大小选择进入还是不进入市场。港口1要根据港口2进入成本的大小,选择对港口2的策略。如果港口2的进入成本满足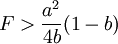 ,在这种情况下,港口1选择产量的范围如果满足
,在这种情况下,港口1选择产量的范围如果满足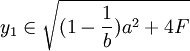 ,
,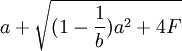 ,此时港口1的资本投资存量为K1 = f − 1(Y1),港口1的资本量构成了进入壁垒,阻止了港口2的进入;如果港口2的进入成本满足
,此时港口1的资本投资存量为K1 = f − 1(Y1),港口1的资本量构成了进入壁垒,阻止了港口2的进入;如果港口2的进入成本满足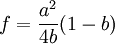 ,则港口1只需常量调整为y1 = a,就能使得港口2即使进入市场,其获得的利润为π2 = 0,但是港口1无论选择除了y1 = a的任何产量,港口2进入市场均会获得利润,此时港口2进入,市场中将会有两个港口,且港口l是领导者,港口2是跟随者;如果港口2的进入成本满足
,则港口1只需常量调整为y1 = a,就能使得港口2即使进入市场,其获得的利润为π2 = 0,但是港口1无论选择除了y1 = a的任何产量,港口2进入市场均会获得利润,此时港口2进入,市场中将会有两个港口,且港口l是领导者,港口2是跟随者;如果港口2的进入成本满足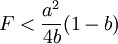 ,此时的进入成本较小,港口1无论怎样选择产量,港口2的进入都会获得利润,此时,市场上将存在港口1、港口2两个港口,港口1是产量领导者,港口2是跟随者,两个港口之间的竞争机制是斯塔克尔博格式的竞争。记
,此时的进入成本较小,港口1无论怎样选择产量,港口2的进入都会获得利润,此时,市场上将存在港口1、港口2两个港口,港口1是产量领导者,港口2是跟随者,两个港口之间的竞争机制是斯塔克尔博格式的竞争。记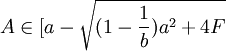
↑ 于谨凯,高磊,刘曙光.基于斯塔克尔伯格模型的港口竞争机制分析——以环渤海港口竞争为例.河北经贸大学学报.2008年11月第29卷第6期
斯塔克尔伯格模型由德国经济学家斯塔克尔伯格(H. Von Stackelberg)在上世纪30年代提出。
在古诺模型和伯特兰德模型里,竞争厂商在市场上的地位是平等的,因而它们的行为是相似的。而且,它们的决策是同时的。当企业甲在作决策时,它并不知道企业乙的决策。但事实上,在有些市场,竞争厂商之间的地位并不是对称的,市场地位的不对称引起了决策次序的不对称,通常,小企业先观察到大企业的行为,再决定自己的对策。德国经济学家斯塔克尔伯格建立的模型就反映了这种不对称的竞争。
该模型的假定是:主导企业知道跟随企业一定会对它的产量作出反应,因而当它在确定产量时,把跟随企业力反应也考虑进去了。因此这个模型也被称为“主导企业模型”。
斯塔克尔伯格模型假设条件
假设厂商1先决定它的产量,然后厂商2知道厂商1的产量后再作出它的产量决策。
因此,在确定自己产量时,厂商1必须考虑厂商2将如何作出反应。
其他假设与古诺模型相同,
斯塔克尔伯格模型分析
斯塔克尔伯格模型是一个价格领导模型,厂商之间存在着行动次序的区别。产量的决定依据以下次序:领导性厂商决定一个产量,然后跟随着厂商可以观察到这个产量,然后根据领导性厂商的产量来决定他自己的产量。需要注意的是,领导性厂商在决定自己的产量的时候,充分了解跟随厂商会如何行动——这意味着领导性厂商可以知道跟随厂商的反应函数。因此,领导性厂商自然会预期到自己决定的产量对跟随厂商的影响。正是在考虑到这种影响的情况下,领导性厂商所决定的产量将是一个以跟随厂商的反应函数为约束的利润最大化产量。在斯塔克尔伯格模型中,领导性厂商的决策不再需要自己的反应函数。
斯塔克尔伯格模型案例分析 ">编辑]案例一:基于斯塔克尔伯格模型的环渤海港口竞争机制分析
一、斯塔克尔伯格港口竞争机制模型
这里所说的港口竞争指的是同一港口群内不同港口之间的竞争。一个区域内往往形成一个港口群,群内港口面临共同的陆向或者海向腹地,因而竞争激烈。港口服务的提供需要具备临海的地理位置,且港口投资的成本大,这些条件的存在限制了港口产业中港口的数量,使得进入港口的产业进入壁垒较大,因而也就决定了港口产业的市场结构。
假设在开始阶段,某区域只有一个港口1,其内陆腹地流出或流向该腹地的所有产品均通过港口1,那么港口1完全垄断市场。假设不存在进入成本,即新港口以任意规模的投资进入均可获得收益,于是潜在进入者港口2可以以任意规模进入市场,并获得利润。下面基于斯塔克尔伯格模型,从产量方面说明港口之间的竞争。
斯塔克尔伯格模型用来描述一个充当领导者角色的厂商与作为追随者的厂商之间的相互影响。假设在所有的港口中存在一个在该行业中处于支配地位的港口,该处于支配地位的港口是斯塔克尔伯格领导者。斯塔克尔伯格领导者对产量的选择将直接导致市场价格的变化,从而影响其他追随者改变自己的产量。同样,处于支配地位的港口产量(对其货物、集装箱的吞吐量的选择)发生变化,供给的变化导致市场价格(港口货物、集装箱装卸、航运价格、泊位费用等费用)变化,而市场价格的变化又促使其他港口改变各自的产量,以保持利润最大化。港口之间博弈的主体是能决定港口产量的政府或者企业。假设条件如下:
1.有两个港口1、2,港口1是产量领导者,产量为y1,港口2是跟随者,即根据港口1的选择而选择产量y2。市场价格是总产量的函数,即p = f(y1 + y2);反需求函数可以认为是p = a − b(y1 + y2)。
2.港口1、2均根据自己的产量确定最大化利润,且两个港口的边际成本为0。
3.由于港口1在整个行业处于支配地位,港口2将在港口1产量确定的情况下实现利润最大化,而港口1也知道港口2根据自己产量确定它的产量,即完全信息。
4.港口2根据港口1确定产量,对港口2而言,港口1的产量是常量,港口1在选择产量时也会考虑到其对港口2的影响。
由于其成本假设为0,港口2的利润函数为:
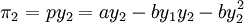 ,
,利润最大化的条件:
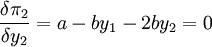 ,
,所以,求得反应函数:
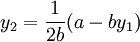
将上面的反应函数代入港口1的利润函数:
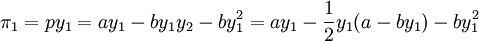
其利润最大化条件:
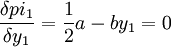
所以均衡时港口1最大利润化的产量
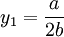
那么,同理可以求出港口2最大利润化的产量:
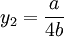
在斯塔克尔伯格模型下均衡时两个港口的产量分别为:
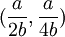 此时港口1、港口2的收益分别为:
此时港口1、港口2的收益分别为: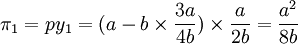
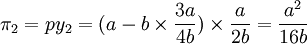
这样,在港口1的产量领导下,港口1和港口2实
现了短期的均衡,均衡时的产量为
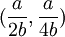 ,市场价格
,市场价格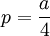 。港口1获得的利润大于港口2的利润,说明了先动者的优势,并且,港口1通过产量的选择限制了港口2的进入规模。
。港口1获得的利润大于港口2的利润,说明了先动者的优势,并且,港口1通过产量的选择限制了港口2的进入规模。二、斯塔克尔伯格港口竞争机制模型的扩展
我们定义港口产量是港口投入资本量的函数,存在下列函数关系:Y=f(K),其反函数K = f − 1(Y)代表港口产量的多少取决于它的资本存量多少。事实上,进入港口行业需要大量的投资,其沉没成本很大,需要较大的进入成本。所以,把进入成本F引入模型,在规模收益递增的情况下,小规模的进入不能获得利润。正是因为进入成本大,才使在位者港口可以遏制其他竞争者的进入。
在进入成本存在的情况下,港口2进入市场后的利润函数变为:
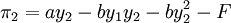
那么,在位者港口1通过制定产量Y1,使得港口2的最大利润满足maxπ2 = 0,这样港口2因进入市场无利可图而不进入,港口1通过产量的选择阻止港口2进入,阻止进人的产量水平由下式确定:
max(ay2 − by1y2 − by − 22 − F)
港口2取得最大利润的条件:
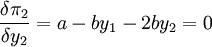
所以,当
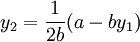 时,港口2的利润最大,最大利润为:
时,港口2的利润最大,最大利润为: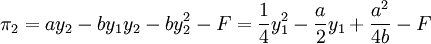
港口1选择自己的产量y1,使港口2的利润
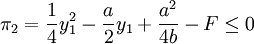
若式子
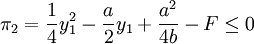 ,即满足
,即满足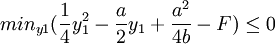
y1 = a时,上式有最小值
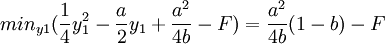
所以,当满足
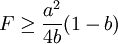 时,港口2利润
时,港口2利润 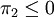
下面分别对几种情况进行讨论:
1. 当
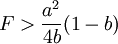 时,
时,y1的取值范围满足
 时,π2 < O;
时,π2 < O;y1取其他值时,π2 > O。
2. 当
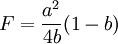 时,y1 = a时,π2 = 0;
时,y1 = a时,π2 = 0;y1取其他值时,π2 > 0。
3. 当
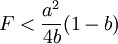 时,π2 > 0。此时,进入壁垒较小,因而不管港口1怎样调整自己的产量,都不能阻止港口2进入市场。
时,π2 > 0。此时,进入壁垒较小,因而不管港口1怎样调整自己的产量,都不能阻止港口2进入市场。由上面的模型可以说明港口之间的竞争机制:在位者根据竞争者进入成本的大小选择遏止其进入还是默许进入策略;而竞争者或者潜在进入者却只能根据其进入成本大小选择进入还是不进入市场。港口1要根据港口2进入成本的大小,选择对港口2的策略。如果港口2的进入成本满足
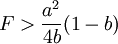 ,在这种情况下,港口1选择产量的范围如果满足
,在这种情况下,港口1选择产量的范围如果满足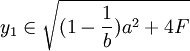 ,
,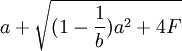 ,此时港口1的资本投资存量为K1 = f − 1(Y1),港口1的资本量构成了进入壁垒,阻止了港口2的进入;如果港口2的进入成本满足
,此时港口1的资本投资存量为K1 = f − 1(Y1),港口1的资本量构成了进入壁垒,阻止了港口2的进入;如果港口2的进入成本满足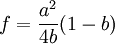 ,则港口1只需常量调整为y1 = a,就能使得港口2即使进入市场,其获得的利润为π2 = 0,但是港口1无论选择除了y1 = a的任何产量,港口2进入市场均会获得利润,此时港口2进入,市场中将会有两个港口,且港口l是领导者,港口2是跟随者;如果港口2的进入成本满足
,则港口1只需常量调整为y1 = a,就能使得港口2即使进入市场,其获得的利润为π2 = 0,但是港口1无论选择除了y1 = a的任何产量,港口2进入市场均会获得利润,此时港口2进入,市场中将会有两个港口,且港口l是领导者,港口2是跟随者;如果港口2的进入成本满足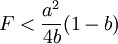 ,此时的进入成本较小,港口1无论怎样选择产量,港口2的进入都会获得利润,此时,市场上将存在港口1、港口2两个港口,港口1是产量领导者,港口2是跟随者,两个港口之间的竞争机制是斯塔克尔博格式的竞争。记
,此时的进入成本较小,港口1无论怎样选择产量,港口2的进入都会获得利润,此时,市场上将存在港口1、港口2两个港口,港口1是产量领导者,港口2是跟随者,两个港口之间的竞争机制是斯塔克尔博格式的竞争。记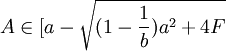
附件列表
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
如果您认为本词条还有待完善,请 编辑
上一篇 数量卡特尔 下一篇 新古典主义经济发展理论
