协方差
什么是协方差
在概率论和统计学中,协方差用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。
期望值分别为E(X) = μ 与 E(Y) = ν 的两个实数随机变量X与Y之间的协方差定义为:
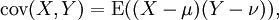
其中,E是期望值。它也可以表示为:
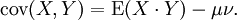
直观上来看,协方差表示的是两个变量总体的误差,这与只表示一个变量误差的方差不同。
如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。
如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
如果X与Y是统计独立的,那么二者之间的协方差就是0。这是因为
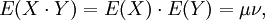
但是,反过来并不成立。即如果X与Y的协方差为0,二者并不一定是统计独立的。
协方差cov(X,Y)的度量单位是X的协方差乘以Y的协方差。而取决于协方差的相关性,是一个衡量线性独立的无量纲的数。
协方差为0的两个随机变量称为是不相关的。
协方差属性
如果X与Y是实数随机变量,a与b不是随机变量,那么根据协方差的定义可以得到:
对于随机变量序列X1, ..., Xn 与 Y1, ..., Ym,有
对于随机变量序列 X1, ..., Xn,有
分别为m与n个标量元素的列向量随机变量X与Y,二者对应的期望值分别为μ与ν,这两个变量之间的协方差定义为m×n矩阵。
两个向量变量的协方差cov(X,Y)与cov(Y,X)互为转置矩阵。
协方差有时也称为是两个随机变量之间“线性独立性”的度量,但是这个含义与线性代数中严格的线性独立性线性独立不同。
在概率论和统计学中,协方差用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。
期望值分别为E(X) = μ 与 E(Y) = ν 的两个实数随机变量X与Y之间的协方差定义为:
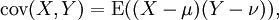
其中,E是期望值。它也可以表示为:
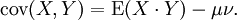
直观上来看,协方差表示的是两个变量总体的误差,这与只表示一个变量误差的方差不同。
如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。
如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
如果X与Y是统计独立的,那么二者之间的协方差就是0。这是因为
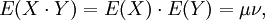
但是,反过来并不成立。即如果X与Y的协方差为0,二者并不一定是统计独立的。
协方差cov(X,Y)的度量单位是X的协方差乘以Y的协方差。而取决于协方差的相关性,是一个衡量线性独立的无量纲的数。
协方差为0的两个随机变量称为是不相关的。
协方差属性
如果X与Y是实数随机变量,a与b不是随机变量,那么根据协方差的定义可以得到:
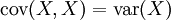
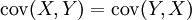
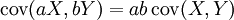
对于随机变量序列X1, ..., Xn 与 Y1, ..., Ym,有
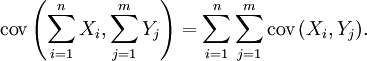
对于随机变量序列 X1, ..., Xn,有
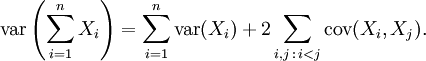
分别为m与n个标量元素的列向量随机变量X与Y,二者对应的期望值分别为μ与ν,这两个变量之间的协方差定义为m×n矩阵。
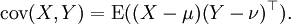
两个向量变量的协方差cov(X,Y)与cov(Y,X)互为转置矩阵。
协方差有时也称为是两个随机变量之间“线性独立性”的度量,但是这个含义与线性代数中严格的线性独立性线性独立不同。
附件列表
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
